Question

A uniform rod of mass ‘m’ and length ‘L’ is held horizontally by two vertical strings attached to the two ends. One of the strings is cut. Find the angular acceleration soon after it is cut:
A. $\dfrac{g}{{2L}}$
B. $\dfrac{g}{L}$
C. $\dfrac{{3g}}{{2L}}$
D. $\dfrac{{2g}}{L}$

Answer 1

When the string is cut, the rod will rotate around the other end which is tied to the string. The torque responsible for the rotation is due to the weight of the rod at the centre of the rod. Use the relation between torque and moment of inertia to solve this question.

Formula used:
The torque is given as,
$\tau = r\,F\sin \theta$
Here, F is the force that causes rotation, r is the position of point of force from the centre of rotation and $\theta$ is the angle between length of the rod and direction of force.
The relation between torque and moment of inertia is,
$\tau = I\alpha$
Here, I is the moment of inertia of the rod and $\alpha$ is the angular acceleration.

Complete step by step answer:
After one of two strings is cut, the rod will move in a circular path around its other end tied to the string as shown in the figure below.

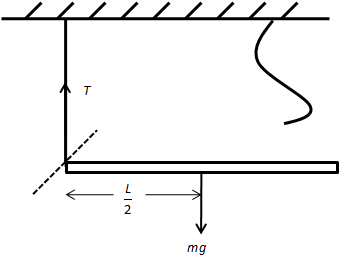
The force which is responsible to rotate the rod around this point is the weight of the rod.
Therefore, the net torque on the rod is due to the weight of the rod which rotates it. The net torque on the rod is,
$\tau = r\,F\sin \theta$
Here, F is the force that causes rotation, r is the position of point of force from the centre of rotation and
$\theta$ is the angle between length of the rod and direction of force.
The angle between length of the rod and weight of the rod is $90^\circ$. The weight is acting at the centre of the rod. Therefore, we can write,
$\tau = mg\left( {\dfrac{L}{2}} \right)$ …… (1)
Here, m is the mass of the rod, g is the acceleration due to gravity and L is the length of the rod.
We know the torque acting on the rod of moment of inertia I is,
$\tau = I\alpha$ …… (2)
Here, I is the moment of inertia of the rod and $\alpha$ is the angular acceleration.
The moment of inertia of the rod with its rotation axis passing through one of the end is,
$I = \dfrac{{m{L^2}}}{3}$
Therefore, equation (2) becomes,
$\tau = \left( {\dfrac{{m{L^2}}}{3}} \right)\alpha$ …… (3)
From equation (1) and (3), we get,
$mg\left( {\dfrac{L}{2}} \right) = \left( {\dfrac{{m{L^2}}}{3}} \right)\alpha$
$\Rightarrow \dfrac{g}{2} = \dfrac{L}{3}\alpha$
$\Rightarrow \alpha = \dfrac{{3g}}{{2L}}$

So, the correct answer is “Option C”.

Note:
The tension in the string also acts on string as one of the forces, but the torque is zero when the force acts at the centre. The angular acceleration and linear acceleration of the rod is different. The linear acceleration is the tangential acceleration of the rod given by $\alpha L$.