Question: A uniform rod of mass m and length l can rotate in vertical plane about a smooth horizontal axis hin...

Question

A uniform rod of mass m and length l can rotate in vertical plane about a smooth horizontal axis hinged at point H. The force exerted by the hinge just after the rod is released from rest is $\dfrac{mg\sqrt{x}}{5}$ . Find the value of x.

Answer 1

Solution

Hint: We will first imagine an infinitesimal length of the rod. Then we will find the force of this infinitesimal mass on the hinge. Then after integrating the force we will find the total force and solve this problem.

Formula used:
$\cos\theta =\sin(90-\theta)$

Complete step-by-step solution:

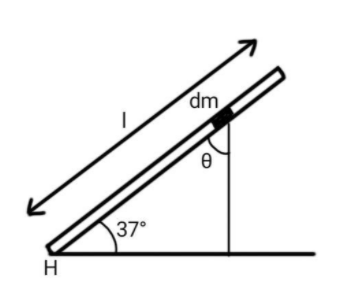
Let's imagine an infinitesimal mass dm. Its force along the vertical line is given by $g.dm$ . The component of this force on the hinge H is $dm.g.\cos\theta$ . Here, $\theta$ is the angle between the rod and the vertical line passing through dm. So, plainly from the concept of geometry we obtain that, $\theta =90-37=53{}^\circ$ . Have a look at the image to have a better understanding of this. So, the expression for the infinitesimal force is given as,
$dF=g.dm.\cos\theta$
Now, the value of $\theta$ is the same for the whole rod. Also, the value of acceleration due to gravity is the same for the whole rod. To get the total force, we have to integrate the above expression for the whole rod. So, after integration the total force is given by,
$F=g.\cos\theta.\int dm=mg.\cos\theta$
Now, we have the value of $\theta$ as 53° . The value of $\cos 53^\circ$ is approximately 0.6. So, the total force is given by,
$F=0.6 \times mg$
So, we have to equal this expression to the given expression that we find in the question. After doing that we can see,
$\dfrac{\sqrt{x}}{5}=0.6$
After solving this, we find the value of x to be 9. So, this is the required value and 9 is the final answer.

Note: It is not possible to remember the sine and cosine values of all the angles. So, try to remember the values of nearby angles, and then try to put an approximate value. Be very careful about which one is the sine and cosine component of a force. You can also convert angle 53 into (90-37) and substitute the value accordingly.