Question

A uniform rod of length l is symmetrically placed on two walls as shown in the figure. The rod is in equilibrium. If ${{N}_{1}}$ and ${{N}_{2}}$ are the normal forces exerted by the walls on the rod then:

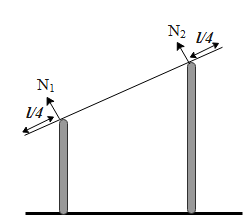
$\begin{aligned} & a){{N}_{1}}>{{N}_{2}} \\\ & b){{N}_{1}}<{{N}_{2}} \\\ & c){{N}_{1}}={{N}_{2}} \\\ & d){{N}_{1}}\text{ and }{{N}_{2}}\text{ would be in vertical directions} \\\ \end{aligned}$

Answer 1

It is given in the above question that the rod is in mechanical equilibrium. It means the rod neither slides down the walls nor it rotates along either walls. Therefore will discuss the necessary conditions for the above rod to be in both the translational and rotational equilibrium. Hence we will conclude the necessary condition for the normal on the rod due to the walls.

Complete answer:
In the above diagram if we see the rod is not sliding down along the incline. Hence we can conclude that the frictional exits between the two walls and the rod. Let us say the coefficient of friction $\mu$ offered by the two walls is the same. Therefore the force of friction due to the either wall not letting the rod to slide down is given as, $F=\mu {{N}_{1}}$ and $F=\mu {{N}_{2}}$. The sliding motion is independent of the normal force due to the rod, as long as the either normal forces are greater than the component of gravitational force making the rod to slide, even one of the normal forces is sufficient enough to hold the rod from sliding down the incline.

Now let us discuss the necessary condition for the rod not to rotate.

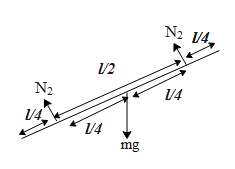
In the above diagram we can see, the two normal forces can act as tangential forces and result in the rotational motion if the torque due to reach of them is not equal. Now since we know that the rod does not slide along the walls, let us say the rod can rotate along its centre of mass i.e. the force due to gravity is mg, where m is the mass of the rod and g is the acceleration due to gravity. The torque acting on a rotating body is given by,

$\tau =r\times F$, where R is the distance from axis of rotation F is the tangential force
$\tau = rF\sin\theta$, where $\theta$ is the angle between r and F

For a body not to rotate along its axis, torque should be in the same direction and the magnitude of the torque should be equal. The two normal forces are in the same direction. Hence further equating the torque due to either normal forces we get,

$\begin{aligned} & \dfrac{l}{4}\times {{N}_{1}}=\dfrac{l}{4}\times {{N}_{2}} \\\ & \dfrac{l}{4}{{N}_{1}}\operatorname{Sin}\theta =\dfrac{l}{4}{{N}_{2}}\operatorname{Sin}\theta \\\ \end{aligned}$
In the above diagram we can see that the length of the rod makes an angle 90 degrees with the normal forces, hence the above equation becomes
$\begin{aligned} & \dfrac{l}{4}{{N}_{1}}=\dfrac{l}{4}{{N}_{2}} \\\ & {{N}_{1}}={{N}_{2}} \\\ \end{aligned}$

So, the correct answer is “Option C”.

Note:
It is to be noted that the rod was not placed symmetrically than the normal forces due to the fact that either walls could no longer be equal in order for the system to be in mechanical equilibrium. The normal forces have to be the same or adjusted such that the system always is in rotational equilibrium. As long as the coefficient of friction is not equal to zero of the either walls and is sufficient enough to overcome the sliding force no condition can be imposed on the normal force due to the two walls.