Question
Question: A uniform rod of length \(l\) is free to rotate in a vertical plane about a fixed horizontal axis th...
A uniform rod of length l is free to rotate in a vertical plane about a fixed horizontal axis through B. the rod begins rotating from rest from its unstable equilibrium position. When it has turned through an angle θ, its angular velocity ω is given by.
A. l6gsin2θ
B. l6gcos2θ
C. l6gsinθ
D. l6gcosθ
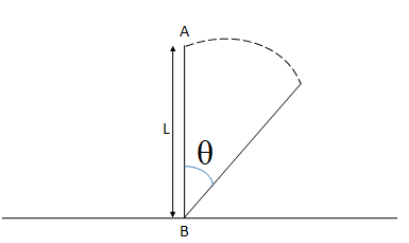
Solution
In this question, we have been asked to determine the angular velocity of a rod that has rotated by an angle theta from the rest position. This problem can be solved by applying the principle of energy conservation. First, determine the potential and kinetic energy separately then from the conservation of energy equate both the energies. Using this method one can determine the value of angular velocity.
Complete step by step answer:

When the rod rotates, we notice that the center of mass also has shifted. We can calculate the new center of mass using the trigonometric expression,
cosθ=hypotenuseadjacent side
⇒cosθ=2Ladjacent side
⇒adjacent side=2Lcosθ
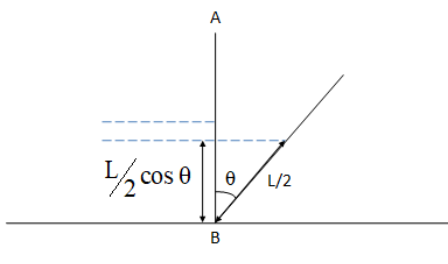
Now the fall in the center of mass is given by h ,
h=2L−2Lcosθ
Simplifying the expression we get,
h=2L(1−cosθ)
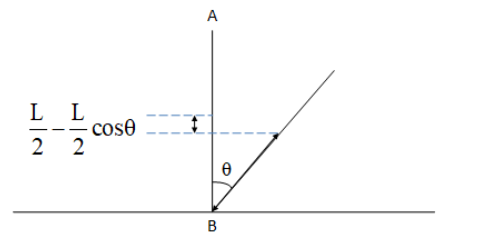
The centre of mass of the rod is given by 2L. While the rod rotates there appears to be a change in the position of the center of mass. This is easily visible in the figures. Therefore the difference in the centre of mass is given by,
h =2L(1−cos θ)
The potential energy of the system can be calculated using the relation mgh , where m is the mass, g is the acceleration due to gravity and h is the height.
Therefore by substituting the value of h we get the potential energy of the rod to be equal to,
Potential energy =mgh =mg2L(1−cos θ)
We know that the rotational kinetic energy can be calculated using the formula 21Iω2, where I is the inertia and ω is the angular velocity.Now we know that the inertia of a rod, when the axis of the rod is through the end of the rod, is given by 3mL2. Now by using the conservation of energy we can solve this problem. That is here, the decrease in the potential energy is equal to the rotational kinetic energy.
21Iω2=mg2L(1−cosθ)
Now substitute the value of inertia in the above equation
21×3mL2×ω2=mg2L(1−cosθ)
Simplifying the above expression we get,
3L×ω2=g(1−cosθ)
⇒ω2=L3g(1 - cos \theta)
⇒ω2=L3g×2sin22θ
∴ω=L6gsin2θ
Hence, option (A) is the correct option.
Note: From the above passage, we have determined the value of angular velocity using the principle of conservation of energy. According to this principle, the energy of interacting bodies remains constant. Basic formulas from trigonometry have been employed to determine the angular velocity of the rod that has rotated from its rest position.
