Question

A uniform rod of length $L$ is free to rotate in a vertical plane about a fixed horizontal axis through $O$. The rod is allowed to rotate from its unstable vertical position. Find the angular velocity of the rod when it has turned through an angle $\theta$.

Answer 1

In this question, we will apply the concept of the law of conservation of mechanical energy. Then we will find the change of centre of gravity and ten we will find the change in potential energy that takes place and then in the end, we will equate it to the kinetic energy to find the answer.

Complete step by step answer:
Here, we are given a uniform rod of whose length is $L$ and it is free to rotate in a vertical plane about a fixed axis passing through $B$. This rotation of the given rod starts from its unstable equilibrium position. We have to find the angular velocity $\omega$ when the rod is turned with an angle equal to $\theta$.

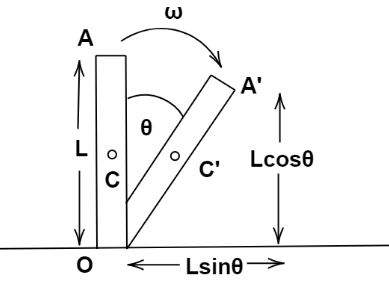
Mechanical energy is defined as the sum of kinetic and potential energy. In this case, the mechanical energy of this system is conserved.The centre of gravity gets shifted from its initial position. The length is,
$h = \dfrac{L}{2} - \dfrac{L}{2}\cos \theta \\\ \Rightarrow h = \dfrac{L}{2}\left( {1 - \cos \theta } \right).......(1)$
The change in potential energy is given by,
$\Delta PE = mgh \\\ \Rightarrow \Delta PE = mg\dfrac{L}{2}\left( {1 - \cos \theta } \right)......(2)$

We also know that rotational kinetic energy is,
$KE = \dfrac{1}{2}I{\omega ^2}$
The moment of inertia of this rod is,
$I = \dfrac{{m{L^2}}}{3}$
$\Rightarrow KE = \dfrac{{m{L^2}{\omega ^2}}}{6}......(3)$
Here, we can equate equation (2) and (3) as this is a conservative system.
$mg\dfrac{L}{2}(1 - \cos \theta ) = \dfrac{{m{L^2}{\omega ^2}}}{6}$
$\Rightarrow {\omega ^2} = \dfrac{{3g(1 - \cos \theta )}}{L} \\\ \Rightarrow {\omega ^2} = \dfrac{{6g{{\sin }^2}\dfrac{\theta }{2}}}{L}$
$\therefore \omega = \sqrt {\dfrac{{6g}}{L}} \sin \dfrac{\theta }{2}$

Therefore, the angular velocity of the rod when it has turned through an angle $\theta$ is $\sqrt {\dfrac{{6g}}{L}} \sin \dfrac{\theta }{2}$.

Note: In this question, we have not taken the translational kinetic energy into consideration as it does not exist here. The point at which the rod is being hinged does not move and thus, we have not taken translational motion into consideration.