Question

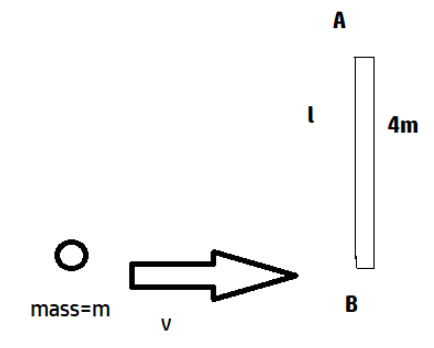
A uniform rod of length L and mass 4m lies on a frictionless horizontal surface on which it is free to move anyway. A ball of mass m moving with speed v as shown in figure collides with the rod at one of the ends. If the ball comes to rest immediately after collision with the rod then find out angular velocity ω of the rod just after the collision.

Answer 1

This problem involves collision and there is no loss of energy during the collision. Also, there is no friction present on the ground. It makes a simple problem of energy conservation.

Complete step by step answer:
In this problem the ball strikes the rod and after collision it comes to rest. Since there is no loss of energy in the form of heat or sound, the entire energy of the ball is transferred to the road. Hence, we can use the law of conservation of angular momentum to solve this problem because the second body starts to rotate around its own axis; the rod is uniform and hence the mass is uniformly distributed. The mass of the rod is 4m and the length of the rod is l. The rod is pivoted at the centre and as soon as the ball strikes the rod at one of its ends it comes to halt and in such a collision all the energy of the ball has been transferred to the road and the rod starts rotating about the centre. We choose the origin of the system at the centre of mass of the rod AB.
Initially, the rod is at rest and the ball is moving so initial angular momentum of the system is given by
${{L}_{i}}=m\overrightarrow{v}\times \overrightarrow{r}=mv\dfrac{l}{2}\sin (90)=mv\dfrac{l}{2}$
After the Collision, the ball stops but the rod and now the rod starts rotating about its centre of mass.
Final angular momentum of the system is given by ${{L}_{f}}=I\omega$
Here $I$is the moment of inertia of rod and its value is $\dfrac{4m{{l}^{2}}}{12}$
So final angular momentum of the system is ${{L}_{f}}=\dfrac{4m{{l}^{2}}\omega }{12}$
Since no external force acts on the system angular momentum remains conserved.
${{L}_{i}}={{L}_{f}}$
$\dfrac{mvl}{2}=\dfrac{4m{{l}^{2}}\omega }{12}$
$\omega =\dfrac{3v}{2l}$

Note: This problem can be solved by using other formulas involving angular momentum but the concept will remain the same. Also, we have to take the moment of inertia of the body given, we should keep in mind different bodies have different moments of inertia. Also the moment of inertia depends upon the axis of rotation around which it is being calculated.