Question

A uniform rod of length $8a$ and mass $6m$ lies on a smooth horizontal surface. Two-point masses $m$ and $2m$ moving in the same plane with speed $2v$ and $v$ respectively strike the rod perpendicularly at a distance $a$ and $2a$ from the mid-point of the rod in the opposite directions and stick to the rod. The angular velocity of the system immediately after the collision is:
$\begin{aligned} & (A)\dfrac{6v}{32a} \\\ & (B)\dfrac{6v}{33a} \\\ & (C)\dfrac{6v}{40a} \\\ & (D)\dfrac{6v}{41a} \\\ \end{aligned}$

Answer 1

Since both the point masses stick to the rod after striking it, the angular momentum of the whole system that is the rod plus the two-point masses shall have the same angular momentum. Therefore, we can apply the Principle of Conservation of Angular Momentum about any point on the rod.

Complete answer:
The given problem can be analyzed using the following diagram:

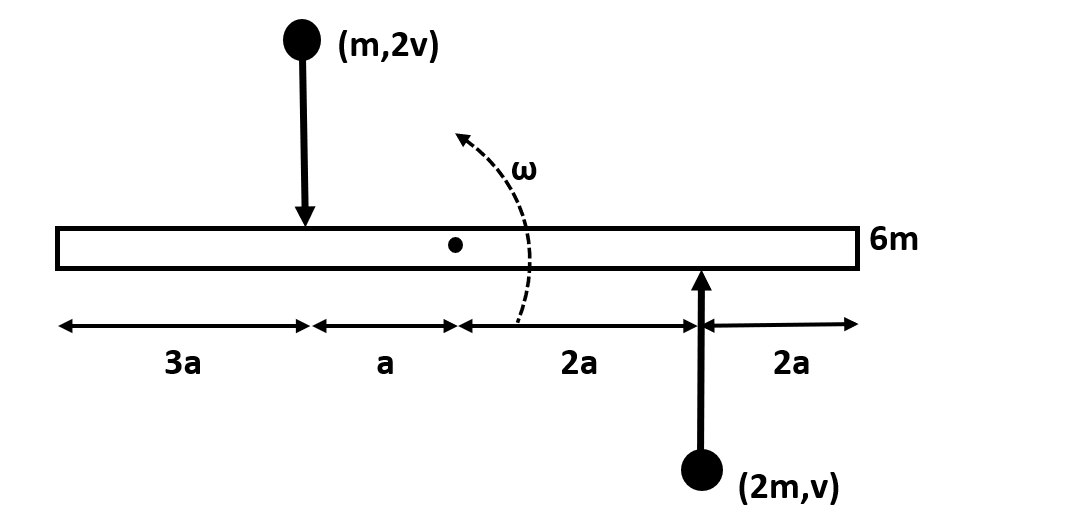
Let us assume the angular momentum of the rod after being struck by the two-point masses to be $\omega$ and let us calculate the angular momentum about the center of the rod before and after collision.
Initially only the two-point masses contribute to the angular momentum of the system and it can be given by:
$\Rightarrow {{L}_{i}}=(m\times 2v\times a)+(2m\times 2v\times a)$
$\Rightarrow {{L}_{i}}=6mva$ [Let this expression be equation number (1)]
Now, after the point masses have struck the rod, the final angular momentum of the system will be the individual sum of $I\omega$ of the two-point masses and the rod. This is equal to:
$\Rightarrow {{L}_{f}}={{I}_{m}}\omega +{{I}_{2m}}\omega +{{I}_{rod}}\omega$
Where,
$\Rightarrow {{I}_{m}}=m{{a}^{2}}$
$\Rightarrow {{I}_{2m}}=2m{{(2a)}^{2}}$
$\Rightarrow {{I}_{rod}}=\dfrac{6m{{(8a)}^{2}}}{12}$
Putting these values in the above equation, we get:
$\Rightarrow {{L}_{f}}=m{{a}^{2}}\omega +8m{{a}^{2}}\omega +32m{{a}^{2}}\omega$
$\Rightarrow {{L}_{f}}=41m{{a}^{2}}\omega$ [Let this expression be equation number (2)]
Equating equation number (1) and (2) using conservation of angular momentum, we get:
$\begin{aligned} & \Rightarrow 6mva=41m{{a}^{2}}\omega \\\ & \Rightarrow \omega =\dfrac{6v}{41a} \\\ \end{aligned}$
Hence, the angular velocity of the system comes out to be $\dfrac{6v}{41a}$.

Hence, option (D) is the correct option.

Note:
In problems like these, if finally the system moves together as one then it’s easier to calculate the angular velocity and angular momentum by applying the principle of conservation of angular momentum rather than finding all the terms separately. It also helps us save our time from unnecessary calculations.