Question

A uniform rod of 20 kg is hanging in a horizontal position with the help of two threads. It also supports a 40 kg mass as shown in the figure. Find the tensions developed in each thread.

Answer 1

We will draw a free body diagram. We will calculate tension in string using translational equilibrium using $\Sigma F = 0$. Then using rotational equilibrium $\tau = 0$, we will calculate individual tensions at point C and D.

Complete step by step answer:

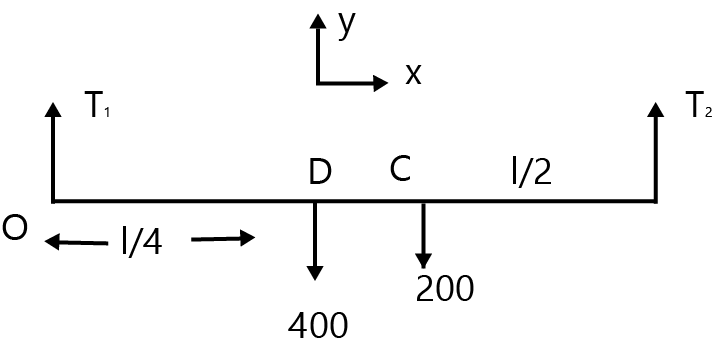
Free body diagram is shown in the figure.
Translational Equilibrium:
A body moving with constant velocity or no acceleration. Then it is said to possess translational equilibrium.
$\Sigma F = 0$
$\Rightarrow \Sigma \,m\,a = 0$
$\Rightarrow a = 0$
$\Rightarrow \dfrac{{dv}}{{dt}} = 0$
$v = const$
Rotational Equilibrium:
A body experiencing a constant rotational velocity or no angular acceleration.
$\Sigma \tau = 0$
$\Sigma \,r \times F = 0$
$F = 0$
In this case object shows a rotational motion in only one direction at a constant angular velocity
$\omega = 0$
According to translational equilibrium
$\Sigma {F_y} = 0$
$\Rightarrow {T_1} + {T_2} = 0$
${T_1}$= tension in string where 40 kg mass is hanged at a distance of $\dfrac{l}{4}$
${T_2}$= tension in string lying at a distance of $\dfrac{l}{2}$ at point C as shown in figure.
$= 40 \times 10 + 20 \times 10$
$= 400 + 200N$
$= 600N$
According to rotational equilibrium
Applying at A, we get
${\tau _A} = 0$
$\Rightarrow - 400\,(l/4) - 200(l/2) + {T_2}l = 0$
${T_2} = 200N$
${T_1} = 100N$

Therefore, tension in string AB is 600 N and tensions at point D and C is 200 N and 100 N respectively.

Note:
If value of g is taken as $9.8\,\dfrac{m}{{{{\sec }^2}}}$instead of $10\dfrac{m}{{{{\sec }^2}}}$ then values would have been different. If the object would have been accelerating then there would be no equilibrium.
Since the direction in which force is acting at point C and D is opposite to point A and B do opposite signs will be used while doing calculation. Negative signs used while calculating torque indicates direction.