Question

A uniform rod OB of length 1m, cross-sectional area $0.012\,{m^2}$ , and relative density $2$ is free to rotate about O in the vertical plane. The rod is held with a horizontal string AB which can withstand a maximum tension of $45\;N$ . The rod and string system is kept in water as shown in the figure. The maximum value of angle $\alpha$ which the rod can make with vertical without breaking the string is

A) $45^\circ$
B) $37^\circ$
C) $53^\circ$
D) $60^\circ$

Answer 1

For the rod to remain stationary, the tension in the string must be compensated by the weight of the rod. The weight of the rod on the other hand will be lowered in the water due to the buoyant force acting on it.

Formula used
In this solution, we will use the following formula:
-Toque of the rod $\tau = I\alpha$ where $I$ is the moment of inertia and $\alpha$ is the angular acceleration
-Relation of force and torque: $\tau = F.r$ where $r$ is the distance from the axis where the force is acting
- Buoyant force of an object: ${F_b} = \rho Vg$ where $\rho$ is the density of the fluid, $V$ is the volume, and $g$ is the gravitational acceleration

Complete step by step answer:
In the situation given to us, we want to find the angle which the rod can make with the vertical. The apparent weight of the rod in this case will be the actual weight of the rod subtracted by the buoyant force acting on the rod.
The actual weight of the rod will be $W = mg = {\rho _r}Vg$ where ${\rho _r}$ is the density of the rod. The volume of the rod will be $V = Al$ where $A$ is the cross-sectional area of the rod and $l$ is the length of the rod. The density of the rod will be the product of the relative density and density of water as $\rho = 2 \times {10^3}$ . So, the weight will be
$W = 0.0012 \times 1 \times 2 \times {10^3} \times 10$
$\Rightarrow W = 240\,N$
The buoyant force on the rod will be
${F_b} = 0.0012 \times 1 \times {10^3} \times 10$
$\Rightarrow {F_b} = 120\,N$
Hence the torque about point O will be due to net force/weight of $(W - {F_B}) = 120\,N$ . This force will have a downwards direction as shown in the figure below.

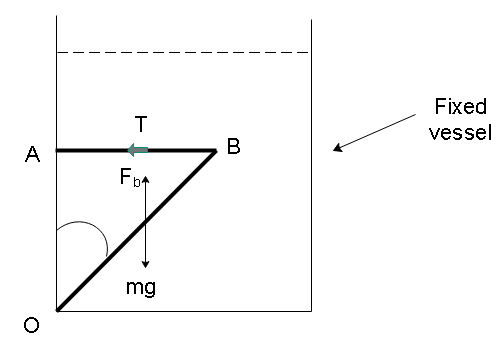
It will also act in the centre of the rod. So, its distance from O will be $l/2$ . The component of length in the direction of the sting will be $\dfrac{l}{2}\sin \alpha$ .
The force in the direction of the string will have to be compensated by the tension in the string. Since the component of length in the direction of the string will be $l\cos \alpha$ , we can write the force balance equation as
$T(l\cos \alpha ) = 120\left( {\dfrac{l}{2}\sin \alpha } \right)$
Solving for $\alpha$ by dividing both sides by $l\cos \alpha$ , we can write
$\tan \alpha = 0.75 = \dfrac{3}{4}$
Which gives us
$\alpha = 37^\circ$
Hence the correct choice is option (B).

Note:
While calculating the weight of the rod, we must ensure that it acts on the centre of mass of the rod and calculate its distance from the point where the string is attached. Also, the torque produced due to the tension in the string will only act on the component of the length in the direction of the string which we must take into account.