Question

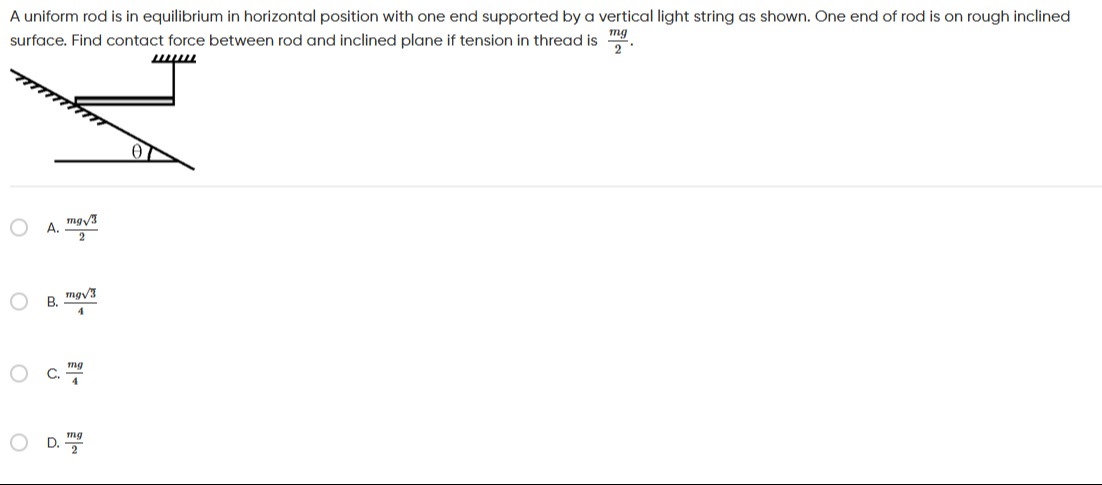
A uniform rod is in equilibrium in horizontal position with one end supported by a vertical light string as shown. One end of rod is on rough inclined surface. Find contact force between rod and inclined plane if tension in thread is $\frac{mg}{2}$.

• A. $\frac{mg\sqrt{3}}{2}$
• B. $\frac{mg\sqrt{3}}{4}$
• C. $\frac{mg}{4}$
• D. $\frac{mg}{2}$

Answer 1

Answer: (D)

$\frac{mg}{2}$

Answer 2

The rod is uniform and in equilibrium in a horizontal position. Let the mass of the rod be $m$ and its length be $L$. The weight $mg$ acts at the center of the rod. The rod is supported by a vertical string at one end (let's call it B) with tension $T = \frac{mg}{2}$, and the other end (let's call it A) rests on a rough inclined surface. Let the angle of inclination of the surface with the horizontal be $\theta$.

The forces acting on the rod are:

1. Weight $mg$ acting vertically downwards at the center of the rod.
2. Tension $T$ acting vertically upwards at end B.
3. Contact force at end A, which can be resolved into a normal force $N$ perpendicular to the inclined plane and a frictional force $f$ parallel to the inclined plane.

We analyze the equilibrium of the rod. Let's resolve all forces into horizontal and vertical components. We set up a coordinate system with the x-axis horizontal and the y-axis vertical.

The weight vector is $\vec{W} = (0, -mg)$. The tension vector is $\vec{T} = (0, T) = (0, \frac{mg}{2})$.

The inclined plane makes an angle $\theta$ with the horizontal. The normal force $N$ is perpendicular to the inclined plane. Assuming the inclined plane is tilted upwards to the right, the normal force acts upwards and to the left. Its components are: $\vec{N} = (-N \sin\theta, N \cos\theta)$.

The frictional force $f$ is parallel to the inclined plane. For equilibrium, let's assume it acts up the incline, i.e., to the right and upwards. Its components are: $\vec{f} = (f \cos\theta, f \sin\theta)$.

For translational equilibrium, the sum of forces in the horizontal and vertical directions must be zero.

Horizontal equilibrium: $f \cos\theta - N \sin\theta = 0 \quad \implies \quad f = N \tan\theta$.

Vertical equilibrium: $N \cos\theta + f \sin\theta + T - mg = 0$. Substitute $T = \frac{mg}{2}$ and $f = N \tan\theta$: $N \cos\theta + (N \tan\theta) \sin\theta + \frac{mg}{2} - mg = 0$ $N \cos\theta + N \frac{\sin^2\theta}{\cos\theta} = mg - \frac{mg}{2}$ $N \left( \frac{\cos^2\theta + \sin^2\theta}{\cos\theta} \right) = \frac{mg}{2}$ $N \left( \frac{1}{\cos\theta} \right) = \frac{mg}{2}$ $N = \frac{mg}{2} \cos\theta$.

Now, we find the frictional force: $f = N \tan\theta = \left(\frac{mg}{2} \cos\theta\right) \tan\theta = \frac{mg}{2} \sin\theta$.

The contact force between the rod and the inclined plane is the vector sum of the normal force $\vec{N}$ and the frictional force $\vec{f}$. The magnitude of the contact force, $F_c$, is given by: $F_c = \sqrt{N^2 + f^2}$ $F_c = \sqrt{\left(\frac{mg}{2} \cos\theta\right)^2 + \left(\frac{mg}{2} \sin\theta\right)^2}$ $F_c = \sqrt{\left(\frac{mg}{2}\right)^2 (\cos^2\theta + \sin^2\theta)}$ $F_c = \sqrt{\left(\frac{mg}{2}\right)^2 \times 1}$ $F_c = \frac{mg}{2}$.

The magnitude of the contact force is $\frac{mg}{2}$, which is independent of the angle $\theta$.