Question
Question: A uniform rod \(AB\) which is free to swing in the vertical plane about a horizontal axis through \(...
A uniform rod AB which is free to swing in the vertical plane about a horizontal axis through A, hanging freely. A particle of equal mass strikes the rod with a velocity vo and gets stuck to it. Find the angular velocity of the combination immediately after the collision.
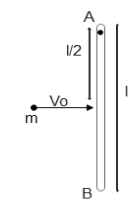
Solution
We are given a rod that is free to swing in the vertical plane about a horizontal axis. It is then collided upon by a mass of a certain velocity and it gets stuck to the rod and we need to find the angular velocity after the collision.
Complete step by step answer:
Since no external torque is applied to the body, therefore, the angular momentum will be conserved about point A after and before the collision of the system.Hence we can write
L1=L2
Where L1 is the angular momentum of the system when the mass was away from the rod and was approaching it and L2 is the angular momentum of the system when the mass gets stuck to the rod.
Therefore substituting the values we get
I1×0+mvo2l=I2×ω−−−−(1)
Since L=mvr=Iω and the distance of the mass particle from the point is given in the figure as half the length of the rod. The initial angular momentum of the rod will be zero
Now we that the moment of inertia about the end of the rod is equal to
I1=31ml2
Where m is the mass of the rod as well as the particle
And the moment of inertia of the particle about point A will be equal to 4ml2
Therefore the moment of the inertia of the system after the mass is tuck to it will be
I2=4ml2+3ml2
⇒I2=127ml2
Therefore the substituting the value in equation 1) we get
mvo2l=127ml2×ω
∴ω=7l6vo
Which is the required expression for the angular velocity of the particle mass just after the collision.
Note: When no external torque is applied to a rotating system then its angular momentum is conserved which means no change will occur in its angular momentum. The moment of inertia of a body is its tendency to resist angular acceleration, which is the sum of the products of the mass of each particle in the body with the square of its distance from the axis of rotation.
