Question

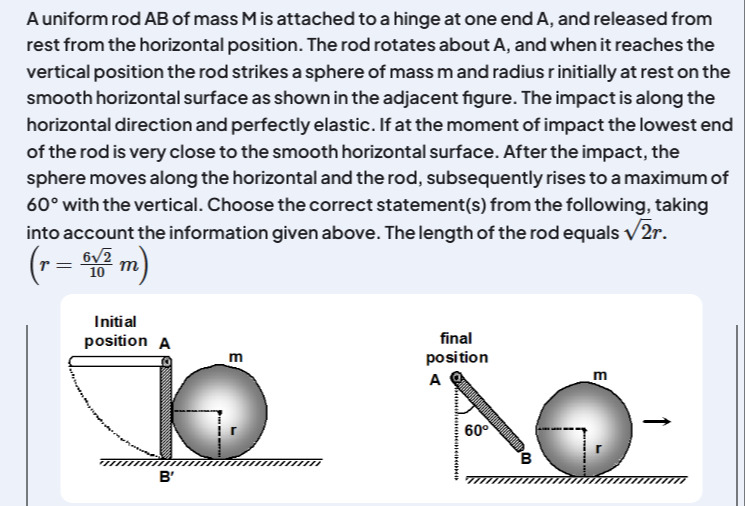
A uniform rod AB of mass M is attached to a hinge at one end A, and released from rest from the horizontal position. The rod rotates about A, and when it reaches the vertical position the rod strikes a sphere of mass m and radius r initially at rest on the smooth horizontal surface as shown in the adjacent figure. The impact is along the horizontal direction and perfectly elastic. If at the moment of impact the lowest end of the rod is very close to the smooth horizontal surface. After the impact, the sphere moves along the horizontal and the rod, subsequently rises to a maximum of 60° with the vertical. Choose the correct statement(s) from the following, taking into account the information given above. The length of the rod equals $\sqrt{2}r$.

$(r = \frac{6\sqrt{2}}{10}m)$

Answer 1

The rod’s mass and the sphere’s mass are related by M/m = 9 + 6√2.

Answer 2

We will show that by applying energy conservation for the swing of the rod after collision together with conservation of angular momentum (about the hinge A) and of kinetic energy in the elastic impact, one finds a relation between M and m. (All steps assume that the rod’s length is L = √2·r, and that at impact the rod is vertical so that its tip B has a horizontal velocity.)

Step 1. Motion of the rod before collision

When the rod is released from the horizontal position (with A fixed) it rotates and, by the time it reaches the vertical position its center‐of‐mass has dropped. (A little thought shows that if the rod is imagined to be initially horizontal with A at the end, then its center of mass will drop by L/2 by the time it is vertical.) Thus energy conservation gives

  (Mg)(L/2) = (½)I₍A₎ω²    (1)

Since for a uniform rod about an end,   I₍A₎ = (1/3)ML², equation (1) gives   (½)(1/3)ML² ω² = MgL/2 ⟹ ω² = (3g)/L.
Thus at collision the tip B (distance L from A) moves horizontally with   v_B = ωL = √(3gL).

Step 2. Collision analysis

At the moment of impact the rod (as a rigid body) collides elastically with a sphere (mass m) at B. Taking A as the axis (through which the impulsive hinge forces have no moment) we have:

a) Angular momentum conservation about A:

Before collision the rod’s angular momentum is   Iω. After collision the rod rotates with angular speed ω′ and the sphere gains a horizontal speed u (its angular momentum about A is m u L); hence   I ω = I ω′ + m u L.    (2)

b) Kinetic energy conservation (elastic collision):

Before collision : K_i = (½)I ω².
After collision : K_f = (½)I ω′² + (½) m u².    (3)

Step 3. Using the swing of the rod after collision

After the collision the rod swings upward reaching a maximum angle 60° with the vertical. (Here the rod’s rotational energy is converted into gravitational potential energy of its center‐of‐mass.)

When vertical the center of mass is L/2 below A. At 60° with the vertical the vertical distance is   (L/2) cos(60°) = L/4. Thus the center‐of‐mass rises by L/2 − L/4 = L/4. Therefore, from energy conservation for the rod’s swing,   (½)I ω′² = Mg (L/4).    (4) Substitute I = (1/3)ML²:   (¼)(1/3)ML² ω′² = Mg (L/4) ⟹ (1/6)ML² ω′² = MgL/4 ⟹ ω′² = (3g)/(2L).
So,   ω′ = √[3g/(2L)].

Step 4. Finding u and the mass–ratio M/m

Now, return to the collision equations. From (2):   m u L = I (ω − ω′), so that   u = [I(ω − ω′)]/(mL) = [(1/3)ML² (ω − ω′)]/(mL) = (M L (ω − ω′))/(3m).

We already found:   ω = √(3g/L)  and  ω′ = √[3g/(2L)] = √(3g/L)/√2. Thus,   ω − ω′ = √(3g/L)[1 − 1/√2].

So the sphere’s speed from (2) is:   u = (M/(3m)) √(3gL) [1 − 1/√2].    (5)

On the other hand, from energy conservation (3), we have   (½)I ω² = (½)I ω′² + (½) m u². A short calculation shows that   u² = (M g L)/(2m).    (6)

Now square (5):   u² = (M²/(9m²)) (3gL)[1 − 1/√2]² = (M² g L/(3m²))[1 − 1/√2]². Equate with (6):   (M² g L/(3m²))[1 − 1/√2]² = (M g L)/(2m). Cancel the common factor M g L (assuming nonzero M, m, L):   (M/(3m))[1 − 1/√2]² = 1/2
⟹ M/(3m) = 1/[2(1 − 1/√2)²].
Solve for M/m:   M/m = 3/[2(1 − 1/√2)²].

Now, compute   (1 − 1/√2)² = ((√2 − 1)/√2)² = ( (√2 − 1)² )/2. But (√2 − 1)² = 2 − 2√2 + 1 = 3 − 2√2. Thus,   (1 − 1/√2)² = (3 − 2√2)/2, so that   M/m = 3/[2 · ((3 − 2√2)/2)] = 3/(3 − 2√2).

It is often preferable to rationalize:   M/m = 3/(3 − 2√2) × [(3 + 2√2)/(3 + 2√2)] = [3(3 + 2√2)]/(9 − 8) = 3(3 + 2√2).

That is,   M/m = 9 + 6√2.