Question

A uniform rod AB of mass $m$ and length $l$ are on a smooth horizontal surface. An impulse $J$ is applied to the end B, perpendicular to the rod in the horizontal direction. Speed of the particle P at a distance $\dfrac{l}{6}$ from the centre towards A of the rod after time $t = \dfrac{{\pi ml}}{{12J}}$ is:
A. $2\dfrac{J}{m}$
B. $\dfrac{J}{{\sqrt 2 m}}$
C. $\dfrac{J}{m}$
D. $\sqrt 2 \dfrac{J}{m}$

Answer 1

First of all, we will find the change in momentum. Initially the rod was at rest. We will find the horizontal component of velocity and angular velocity. We will also find the angle by which the rod will be rotated. After finding the vertical component of the velocity, we will find the net velocity.

Formula used:
Impulse which is called the change in momentum is given by:
$J = mv - mu$ …… (1)
Where,
$J$ indicates the impulse.
$m$ indicates the mass of the rod.
$v$ indicates final velocity.
$u$ indicates the initial velocity.
Moment of inertia of a uniform rod is given by:
$I = \dfrac{{m{l^2}}}{{12}}$ …… (2)

Complete step by step answer:
In the given question, we are supplied with the following data:
There is a uniform rod AB, whose mass is $m$ and length $l$ are on a smooth horizontal surface. We apply an impulse $J$ to the end B, perpendicular to the rod in the horizontal direction. We are asked to find the speed of the P at a distance $\dfrac{l}{6}$ from the centre towards A of the rod after time $t = \dfrac{{\pi ml}}{{12J}}$.

To begin with, we have to bring in the concept of linear and angular velocities. For better understanding, we have to draw a diagram in support of the solution.

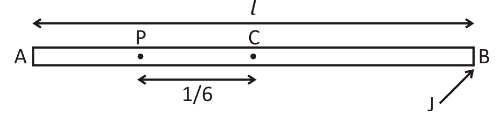
In the diagram, we have clearly shown the position of the particle P at a distance of $\dfrac{l}{6}$ from the centre towards A of the rod. In the figure as we can see that the impulse is applied at the end B.

Let the linear velocity which is applying the impulse be $v$.The angular velocity be $\omega$.We know that impulse is nothing but the change in momentum. Initially, the rod was at rest.
J = mv - m \times 0 \\\ \Rightarrow J = mv \\\ \Rightarrow v = \dfrac{J}{m} \\\
We know from the figure that angular impulse is equal to the change in angular momentum about the point C.
So, we can write:
I\omega = J\dfrac{l}{2} \\\ \Rightarrow \dfrac{{m{l^2}}}{{12}} \times \omega = J\dfrac{l}{2} \\\ \Rightarrow \dfrac{{ml}}{{12}} \times \omega = \dfrac{J}{2} \\\ \Rightarrow \omega = \dfrac{{6J}}{{ml}} \\\
The angular velocity is found to be $\dfrac{{6J}}{{ml}}$.

As we know that after time $t$, the rod will rotate through an angle of say $\theta$.
So, we can write:
\theta = \omega t \\\ \Rightarrow \theta = \dfrac{{6J}}{{ml}} \times \dfrac{{\pi ml}}{{12J}} \\\ \Rightarrow \theta = \dfrac{\pi }{2} \\\
Now, we can find the vertical component of the velocity as:
{v_{\text{p}}} = \dfrac{l}{6} \times \omega \\\ \Rightarrow {v_{\text{p}}} = \dfrac{l}{6} \times \dfrac{{6J}}{{ml}} \\\ \Rightarrow {v_{\text{p}}} = \dfrac{J}{m} \\\
Since, we have both the vertical and horizontal components of the velocities, now we can find the resultant velocity.
{v_{{\text{net}}}} = \sqrt {{v^2} + v_{\text{p}}^2} \\\ \Rightarrow {v_{{\text{net}}}} = \sqrt {{{\left( {\dfrac{J}{m}} \right)}^2} + {{\left( {\dfrac{J}{m}} \right)}^2}} \\\ \therefore {v_{{\text{net}}}} = \sqrt 2 \dfrac{J}{m} \\\
Hence, the speed of the P at a distance $\dfrac{l}{6}$ from the centre towards A of the rod after time $t = \dfrac{{\pi ml}}{{12J}}$ is $\sqrt 2 \dfrac{J}{m}$.

The correct option is D.

Note: While solving this problem, it is important to keep in mind that impulse is nothing, but the change in momentum. It is important to find the angle through which the rod will rotate, as the net velocity of the particle is directly dependent on the angle. Mistakes in finding the angle, will cause irrelevant results in finding the velocity. The vertical component of the velocity is due to the angular rotation of the rod. Larger the magnitude of impulse, larger is the angle by which the rod will rotate.