Question
Question: A uniform rod AB length $\ell$ and mass m is suspended by two identical strings OA and OB from a fix...
A uniform rod AB length ℓ and mass m is suspended by two identical strings OA and OB from a fixed point O as shown in the figure. The rod is in the horizontal position and each string makes an angle θ with the rod. If the string OB is cut, choose the correct option (s) just after the string is cut: (Use θ = 30°)
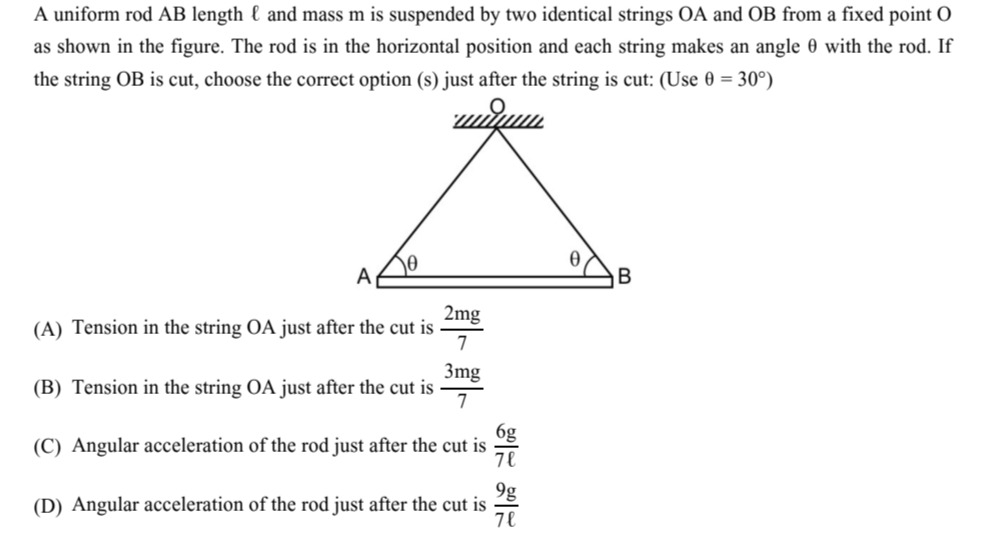
Tension in the string OA just after the cut is 72mg
Tension in the string OA just after the cut is 73mg
Angular acceleration of the rod just after the cut is 7ℓ6g
Angular acceleration of the rod just after the cut is 7ℓ9g
A, C
Solution
The initial state of the rod is equilibrium. The rod AB of length ℓ and mass m is suspended by two identical strings OA and OB from a fixed point O. The rod is horizontal, and each string makes an angle θ with the rod. Let T be the tension in each string.
In the initial equilibrium, the vertical forces balance the weight: 2Tsinθ=mg, so T=2sinθmg. Given θ=30∘, sin30∘=1/2. So, T=2(1/2)mg=mg.
Just after the string OB is cut, the tension in OB becomes zero. The forces acting on the rod are the tension T′ in string OA and the weight mg acting at the center of mass C (midpoint of AB). Let's consider the motion of the rod. Point A is constrained to move on a circle centered at O with radius equal to the length of string OA. Let L be the length of string OA. In the initial configuration, consider the triangle formed by O, A, and the midpoint C of AB. AC = ℓ/2. The angle OAC = θ. Triangle OAC is a right-angled triangle with the right angle at C if OC is vertical and AB is horizontal. From the figure, the angle between the string and the rod is θ. So, angle OAB = angle OBA = θ. In triangle OAC, angle OAC = θ, AC = ℓ/2. L=OA=AC/cosθ=2cosθℓ. Given θ=30∘, cos30∘=3/2. So, L=2(3/2)ℓ=3ℓ.
Just after cutting the string OB, the rod starts to move. Let's apply Newton's laws and rotational dynamics. Let aC be the acceleration of the center of mass C, and α be the angular acceleration of the rod. The net force on the rod is Fnet=T′+mg=maC. The net torque about the center of mass C is τC=ICα. The moment of inertia of a uniform rod about its center is IC=121mℓ2.
Let's choose a coordinate system with origin at O, the fixed point. Let the initial position of O be (0, 0). Since the rod is horizontal and symmetric, the center of mass C is vertically below O. Let the y-axis be vertically downwards. Initially, O is at (0, 0). C is at (0,h) where h=OC. In triangle OAC, h=ACtanθ=(ℓ/2)tanθ. Given θ=30∘, tan30∘=1/3. So h=23ℓ. A is at (−ℓ/2,h) and B is at (ℓ/2,h). The string OA has length L=(−ℓ/2)2+h2=ℓ2/4+ℓ2/12=123ℓ2+ℓ2=124ℓ2=3ℓ2=3ℓ.
Just after cutting OB, O is at (0, 0). Let the coordinates of A be (xA,yA). The tension T′ is along AO, so T′=−T′∣OA∣OA=−T′L(xA,yA). Let the coordinates of C be (xC,yC). The weight is mg=(0,mg). Fnet=T′+mg=maC. −T′LxAi^+(−T′LyA+mg)j^=m(aCxi^+aCyj^).
The torque about C is τC=rCA×T′. rCA=A−C=(xA−xC,yA−yC). τC=ICα.
Let's consider the acceleration constraints. Point A is connected to O by a string, so its acceleration aA must have no component along the string OA. Let u^OA be the unit vector along OA. aA⋅u^OA=0. u^OA=∣A−O∣A−O=L(xA,yA). aA=aC+α×rCA. Initially, the rod is horizontal. Let the angle it makes with the horizontal be ϕ. ϕ=0 initially. Let the angular velocity be ω. ω=0 initially. Let the initial direction of AB be along the x-axis. C is at (xC,yC). A is at (xC−ℓ/2cosϕ,yC−ℓ/2sinϕ). Just after cutting, ϕ=0 and ω=0. Let the acceleration of C be (aCx,aCy) and angular acceleration be α. aA=aC+α×rCA. rCA=(−ℓ/2,0) just after cutting, assuming the rod is along the x-axis through C. α=(0,0,α) if rotation is in xy plane. α×rCA=(0,0,α)×(−ℓ/2,0,0)=(0,−α(−ℓ/2),0)=(0,αℓ/2,0). aA=(aCx,aCy)+(0,αℓ/2)=(aCx,aCy+αℓ/2).
The tension T′ is along AO. The initial position of A relative to O is (−ℓ/2,h). The unit vector along OA is u^AO=L(−ℓ/2,h). The tension T′ is along AO, so T′=T′u^AO=T′L(−ℓ/2,h). Fnet=T′+mg=T′L(−ℓ/2,h)+(0,mg)=m(aCx,aCy). aCx=−2mLT′ℓ and aCy=mLT′h+g.
The torque about C is τC=rCA×T′. rCA=(−ℓ/2,0). T′=T′L(−ℓ/2,h). τC=(−ℓ/2,0,0)×LT′(−ℓ/2,h,0)=(0,0,(−ℓ/2)LT′h−0)=(0,0,−2LT′ℓh). τC=−2LT′ℓh. ICα=τC. 121mℓ2α=−2LT′ℓh. α=−mLL6T′h. The negative sign indicates clockwise angular acceleration if α is taken as positive for counterclockwise. Let's assume positive α for clockwise. α=mLL6T′h.
Constraint: aA⋅u^OA=0. u^OA=L(−ℓ/2,h). aA=(aCx,aCy+αℓ/2). (aCxi^+(aCy+αℓ/2)j^)⋅(−ℓ/2i^+hj^)=0. aCx(−ℓ/2)+(aCy+αℓ/2)h=0. −2mLT′ℓ(−ℓ/2)+(mLT′h+g+αℓ/2)h=0. 4mLT′ℓ2+mLT′h2+gh+2αℓh=0. Substitute α=mLL6T′h. 4mLT′ℓ2+mLT′h2+gh+21ℓhmLL6T′h=0. Multiply by mL: 4T′ℓ2+T′h2+mghL+3T′ℓh2/L=0. This seems wrong.
Let's consider the constraint in terms of acceleration components along and perpendicular to OA. aA=aC+α×rCA. Let's use a coordinate system with origin at A. x-axis along AB, y-axis perpendicular to AB. rAC=(ℓ/2,0). C=A+rAC. aC=aA+α×rAC−ω2rAC. Initially ω=0. aC=aA+α×rAC. Let aA=aAxi^+aAyj^ in this frame. α=(0,0,α). rAC=(ℓ/2,0,0). α×rAC=(0,0,α)×(ℓ/2,0,0)=(0,αℓ/2,0). aC=(aAx,aAy+αℓ/2).
Forces on the rod: T′ along AO, mg at C. T′ makes angle θ with AB. Components are (−T′cosθ,T′sinθ). mg acts vertically downwards. Let's find its components in this frame. The rod is horizontal, so gravity is along −j^. mg=(0,−mg). Fnet=(−T′cosθ,T′sinθ−mg)=m(aCx,aCy). aCx=−mT′cosθ, aCy=mT′sinθ−mg.
Torque about C: τC=rCA×T′+rCC×mg. rCC=0. rCA=(−ℓ/2,0). T′=(−T′cosθ,T′sinθ). τC=(−ℓ/2,0,0)×(−T′cosθ,T′sinθ,0)=(0,0,(−ℓ/2)T′sinθ−0)=−2T′ℓsinθ. ICα=τC. 121mℓ2α=−2T′ℓsinθ. α=−mℓ6T′sinθ. Let's assume positive α for clockwise rotation. α=mℓ6T′sinθ.
Constraint on the motion of A. A is connected to O by a string. The acceleration of A perpendicular to OA is aA⊥OA=LαOA, where αOA is the angular acceleration of the string OA about O. The acceleration of A has no component along OA. Let the direction of OA be u^OA. aA⋅u^OA=0. Initially, the angle between AB and OA is θ. Let's consider the angle of OA with the vertical. In triangle OAC, OC is vertical, AC is horizontal. Angle OAC is θ. Angle OCA = 90∘. Angle AOC = 90∘−θ. The angle of OA with the vertical is 90∘−θ. The angle with the horizontal is θ. Let's use an inertial frame with y-axis vertical upwards and x-axis horizontal. Initial position of A relative to O is (Lcosθ,−Lsinθ) if O is at (0, 0) and AB is horizontal below O. Let's put O at (0, 0). Initial position of A is (xA,yA). String OA makes angle θ with the horizontal rod. The rod is horizontal. Let the rod be at height y below O. y=Lsinθ. Let the horizontal distance from O to C be 0. Then A is at (−Lcosθ,−Lsinθ) and B is at (Lcosθ,−Lsinθ). The length of the rod is 2Lcosθ=ℓ. So L=ℓ/(2cosθ). This matches our previous result. Initial position of A relative to O is (−ℓ/2,−2ℓtanθ). Let O be the origin (0, 0). Initial position of A is (xA,yA)=(−ℓ/2,−2ℓtanθ). The tension T′ is along OA. T′=−T′u^OA=−T′L(xA,yA)=−T′ℓ/(2cosθ)(−ℓ/2,−ℓ/2tanθ)=−T′ℓ/(2cosθ)(−ℓ/2,−ℓ/2sinθ/cosθ)=−T′ℓ/2(−ℓ/2cosθ,−ℓ/2sinθ)=−T′(−cosθ,−sinθ)=T′(cosθ,sinθ). This means the tension makes an angle θ with the horizontal, pointing towards O. This is consistent with the figure if the rod is below O.
Forces on the rod: T′=(T′cosθ,T′sinθ) at A, mg=(0,−mg) at C. Let the acceleration of C be (aCx,aCy) and angular acceleration be α. Fnet=T′+mg=(T′cosθ,T′sinθ−mg)=maC. aCx=mT′cosθ, aCy=mT′sinθ−mg.
Torque about C: τC=rCA×T′. rCA=A−C. Initial position of C is (0,−ℓ/2tanθ). Initial position of A is (−ℓ/2,−ℓ/2tanθ). rCA=(−ℓ/2,0). τC=(−ℓ/2,0,0)×(T′cosθ,T′sinθ,0)=(0,0,−ℓ/2T′sinθ). ICα=τC. 121mℓ2α=−2T′ℓsinθ. α=−mℓ6T′sinθ. Let's take positive α for clockwise rotation. α=mℓ6T′sinθ.
Constraint: Acceleration of A has no component along OA. Initial unit vector along OA is u^OA=∣A−O∣A−O=L(−ℓ/2,−ℓ/2tanθ)=ℓ/(2cosθ)(−ℓ/2,−ℓ/2sinθ/cosθ)=ℓ/2(−ℓ/2cosθ,−ℓ/2sinθ)=(−cosθ,−sinθ). aA=aC+α×rCA. aC=(aCx,aCy). α=(0,0,α). rCA=(−ℓ/2,0,0). α×rCA=(0,0,α)×(−ℓ/2,0,0)=(0,αℓ/2,0). aA=(aCx,aCy+αℓ/2). aA⋅u^OA=(aCxi^+(aCy+αℓ/2)j^)⋅(−cosθi^−sinθj^)=0. −aCxcosθ−(aCy+αℓ/2)sinθ=0. −(mT′cosθ)cosθ−(mT′sinθ−mg+21ℓmℓ6T′sinθ)sinθ=0. −mT′cos2θ−(mT′sinθ−mg+m3T′sinθ)sinθ=0. −mT′cos2θ−(m4T′sinθ−mg)sinθ=0. Multiply by m: −T′cos2θ−(4T′sinθ−mg)sinθ=0. −T′cos2θ−4T′sin2θ+mgsinθ=0. T′(cos2θ+4sin2θ)=mgsinθ. T′(cos2θ+4(1−cos2θ))=mgsinθ. T′(cos2θ+4−4cos2θ)=mgsinθ. T′(4−3cos2θ)=mgsinθ. T′=4−3cos2θmgsinθ. Given θ=30∘, sinθ=1/2, cosθ=3/2, cos2θ=3/4. T′=4−3(3/4)mg(1/2)=4−9/4mg/2=(16−9)/4mg/2=7/4mg/2=2mg×74=72mg. So, the tension in the string OA just after the cut is 72mg. Option (A) is correct.
Now let's find the angular acceleration α=mℓ6T′sinθ. α=mℓ6(72mg)(1/2)=mℓ67mg=7ℓ6g. So, the angular acceleration of the rod just after the cut is 7ℓ6g. Option (C) is correct.
Therefore, the correct options are (A) and (C).
