Question
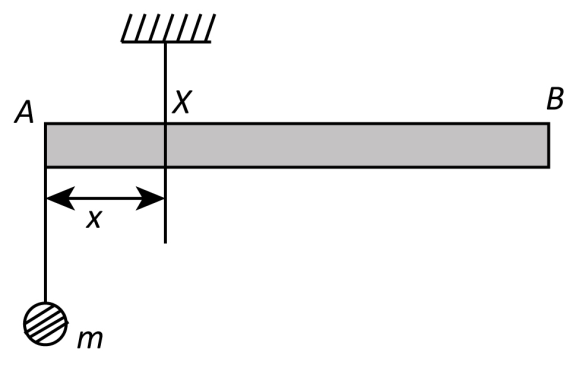
Question: A uniform rod \( AB \) is suspended from a point X, at a variable distance \( x \) from A, as shown....
A uniform rod AB is suspended from a point X, at a variable distance x from A, as shown. To make the rod horizontal, a mass m is suspended from its end A . A set of ( m,x ) values is recorded. The appropriate variables that give a straight line, when plotted, are:
(A) m,x1
(B) m,x21
(C) m,x
(D) m,x2
Solution
Hint : Assume mass and length of the rod and take a moment about point X and compare the equation with the equation of line, y=mx+c .
Complete Step By Step Answer:
From the given question, we know that the A uniform rod AB is suspended from a point X, at a variable distance x from A and mass m is suspended from the end A .
Let us consider the mass of the rod AB be M and length of the rod be L .
The figure below represents the free body diagram of the rod.
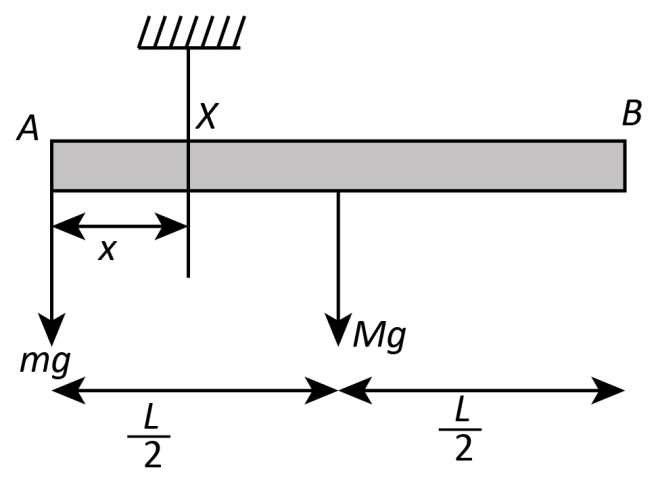
Now for the rod to be in equilibrium (horizontal), we take the moment about its end A ,
We are taking the anti- clockwise direction of the moment as positive.
∑MA=0 mg(x)−Mg(2L−x)=0
Rewrite the above equation.
mg(x)=Mg(2L−x)
mx=(2ML)x1−M ... (I)
We know that the equation of a line is represented by y1=my2+c where y1 and y2 are the variables of two axis’, m is slope and c is the intercept.
Compare the equation of line with equation (I), we get,
y1=m and y2=x1
Thus, the appropriate variables that give a straight line, when plotted, are m and x1 and option (A) is correct.
Note :
While taking the moment, you can assume a counter- clockwise direction as positive and clockwise wise direction is negative, but use assume also assume the opposite. And always the perpendicular distance from the force to the point about which you want to take a moment.
