Question

A uniform rectangular thin sheet ABCD of mass M has length a, and breadth b, as shown in figure. if the shaded portion HBGO is cut off, the coordinates of the centre of mass of the remaining portion will be:

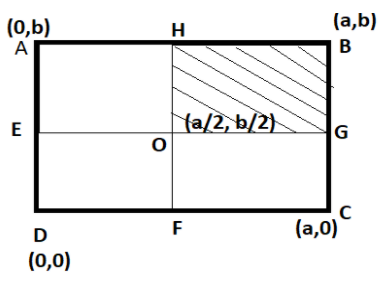
A. (2a/3, 2b/3)
B. (5a/3, 5b/3)
C. (3a/4, 3b/4)
D. (5a/12, 5b/12)

Answer 1

the Centre of mass of a body depends on the spread of mass inside it. The Centre of mass should be calculated from the origin of the body. It lies on the line joining the two or more particles. The Centre of mass at a point is given by the product of individual masses and their respective position vectors.

Formula used:
The centre of mass at a point is given by:
$X=({{m}_{1}}{{r}_{2}}+{{m}_{2}}{{r}_{2}})/({{m}_{1}}+{{m}_{2}})$

Complete answer :
The centre of mass is telling itself by its name as the mass at the centre of a body.
It is defined as the point where the whole mass of the system is concentrated at the centre of a body . The distance of centre of mass of a system of particles from its origin is equal to the product of mass and their respective distances from the origin.
The centre of mass at point X from origin is calculated as:
$X=({{m}_{1}}{{r}_{2}}+{{m}_{2}}{{r}_{2}})/({{m}_{1}}+{{m}_{2}})$
In the question, it is said that one portion of the sheet is cut off, and is represented by shaded portion HBGO. Now, we are left with 3 portions of the thin rectangular sheet having mass M. The figure shows the shaded portion of thin rectangular sheet ABCD.

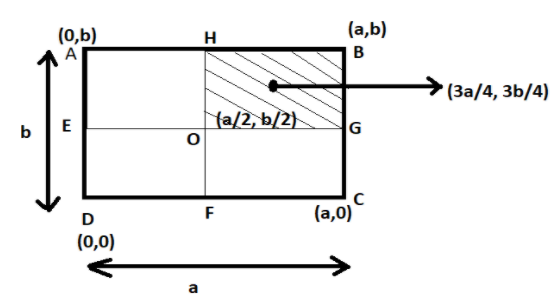
The initial mass of the thin rectangular sheet ABCD is M. The mass on the shaded portion HBGO is M/4.
Now, the coordinates of the centre of mass for the remaining part of the sheet be (X,Y).
Now, calculating centre of mass at point X is:
$\begin{aligned} & X=(M\times (a/2)-(M/4)\times (3a/4))/(M-M/4) \\\ & X=(a/2)-(3a/16)/(3/4) \\\ & X=5a/12 \\\ \end{aligned}$
Where the negative sign in the above equation represents mass will move in the opposite direction.
Now for point Y we have:
$\begin{aligned} & Y=(M\times (b/2)-(M/4)\times (3b/4))/(M-M/4) \\\ & Y=(b/2)-(3b/16)/(3/4) \\\ & Y=5b/12 \\\ \end{aligned}$
Therefore the centre of mass at the remaining portion will be (5a/12, 5b/12).

So, option B is the correct option.

Note:
The centre of mass is the point in the center on which the whole mass of the object is concentrated. The centre of mass is the product of mass and the position vector of that point from origin.