Question
Question: A uniform rectangular solid box of side length \[L\] and width \[w\] is placed on a frictionless inc...
A uniform rectangular solid box of side length L and width w is placed on a frictionless incline of variable angle θ. Assume that there is a very tiny peg preventing the box from sliding down the incline at the point labelled P. At what angle of incline will the box begin to tip over?
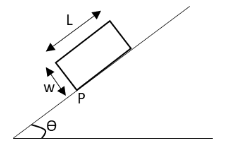
A. θ=sin−1(wL)
B. θ=cos−1(wL)
C. θ=tan−1(wL)
D. θ=cot−1(wL)
Solution
Use the formula for torque acting on an object due to a force acting on the object. The condition for an object to be in equilibrium is the net torque due to all forces on the system is zero. Draw the free body diagram of the rectangular block and determine the net torque acting on the box about an axis passing through the point P. Solve the obtained equation and determine the angle for which the box will begin to tip over.
Formula used:
The torque τ acting on an object due to the force F is given by
τ=Fr …… (1)
Here, r is the perpendicular distance between the point of action of the force and centre of torque.
Complete step by step answer:
We have given that the length and width of the rectangular box placed on a frictionless inclined plane are L and w respectively. The angle made by the inclined plane with the horizontal is θ. The peg placed at point P is preventing the rectangular block from sliding down. We have asked to determine the angle for which the block slides down the inclined plane. Let m be the mass of the rectangular block. Let us first draw the free body diagram of the rectangular block.
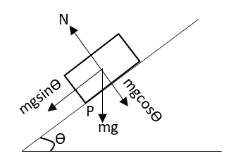
In the above free body diagram, mg is the weight of the rectangular block and N is the normal force exerted by the inclined plane on the block. The components of the weight of the rectangular block are shown in the free body diagram.
The rectangular block will be in equilibrium at point P if the net torque acting on this block about the point P is zero. The torque due to the forces N and mgcosθ will cancel each other. The net torque on the rectangular box about an axis passing through point P is only due to the forces mg and mgsinθ. The torque due to weight mg of the rectangular box is given by
τmg=mg2L
The torque due to the component of weight mgsinθ of the rectangular box is given by
τmgsinθ=−mgsinθ2w
Let us now determine the net torque acting on the rectangular block in equilibrium.
τnet=0
⇒τmg+τmgsinθ=0
⇒mg2L−mgsinθ2w=0
⇒mg2L=mgsinθ2w
⇒L=wsinθ
∴θ=sin−1(wL)
Therefore, the angle of incline for which the box begins to tip over is sin−1(wL).
Hence, the correct option is A.
Note: The students should not forget to use the correct sign for the torque due to different forces acting on the rectangular box as the sign for clockwise torque is negative and sign for counterclockwise torque is positive. Also the torque due to the equal force is zero. Hence, one should not consider the torque due to the equal forces as they will cancel each other.
