Question

A uniform rectangular block is moving to the right on a rough horizontal floor (the block is retarding due to friction). The length of the block is L and its height is h. A small particle (A) of mass equal to that of the block is stuck at the upper left edge. Coefficient of friction between the block and the floor is $\mu = \frac{2}{3}$.

Find the value of h (in terms of L) if the normal reaction of the floor on the block effectively passes through the geometrical centre (C) of the block.

Answer 1

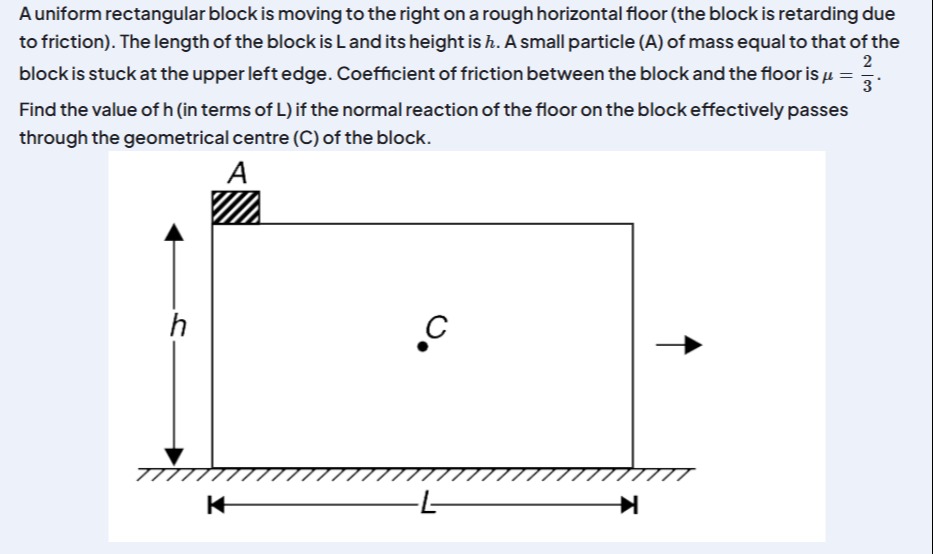
L/2

Answer 2

The problem asks us to find the height 'h' of a uniform rectangular block in terms of its length 'L', given that a particle 'A' of equal mass is stuck at its upper left edge, and the block is retarding due to friction on a rough horizontal floor. The coefficient of friction is $\mu = \frac{2}{3}$. A key condition is that the normal reaction from the floor effectively passes through the geometrical centre (C) of the block.

Let M be the mass of the uniform rectangular block.
The mass of particle A is also M.
The total mass of the system (block + particle A) is $M_{total} = M + M = 2M$.

1. Determine the forces and acceleration:

• Vertical equilibrium: The total weight acting downwards is $M_{total}g = 2Mg$. The normal reaction force N acts upwards. Since there is no vertical acceleration,
  $N = 2Mg$
• Horizontal motion: The block is retarding, meaning it has an acceleration 'a' to the left. The only horizontal force is the kinetic friction $f_k$, acting to the left.
  $f_k = \mu N$
  Applying Newton's second law in the horizontal direction:
  $F_{net, x} = M_{total} a$
  $-f_k = (2M)a$
  $-\mu N = 2Ma$
  Substitute $N = 2Mg$:
  $-\mu (2Mg) = 2Ma$
  $a = -\mu g$
  The magnitude of the acceleration is $a = \mu g$. The negative sign indicates retardation (acceleration is opposite to the direction of motion, which is to the left).

2. Locate the center of mass (CM) of the system:
Let's set up a coordinate system with the origin at the bottom-left corner of the block.

• The center of mass of the uniform block is at $(X_{block}, Y_{block}) = (L/2, h/2)$.
• Particle A is at the upper-left edge, so its coordinates are $(X_A, Y_A) = (0, h)$.

The x-coordinate of the system's CM:
$X_{CM} = \frac{M \cdot (L/2) + M \cdot 0}{M + M} = \frac{ML/2}{2M} = \frac{L}{4}$

The y-coordinate of the system's CM:
$Y_{CM} = \frac{M \cdot (h/2) + M \cdot h}{M + M} = \frac{M(h/2 + h)}{2M} = \frac{3h/2}{2} = \frac{3h}{4}$

So, the center of mass of the system is at $(L/4, 3h/4)$.

3. Apply the torque equation:
The problem states that the normal reaction force N effectively passes through the geometrical centre (C) of the block.
The geometrical center C of the block is at $(L/2, h/2)$. This means the normal force N acts at the point $(L/2, 0)$ on the base of the block. Consequently, the friction force $f_k$ also acts at $(L/2, 0)$.

We need to consider the torques acting on the system. Since the block is undergoing translational acceleration but no angular acceleration (it's not tilting), the net torque about any point P is given by $\vec{\tau}_P = \vec{r}_{CM/P} \times (M_{total} \vec{a}_{CM})$. Here, $\vec{r}_{CM/P}$ is the position vector of the CM relative to point P.

Let's choose point P as the geometrical center C of the block, at $(L/2, h/2)$.
The acceleration of the CM is $\vec{a}_{CM} = -a \hat{i} = -\mu g \hat{i}$ (since 'a' is to the left).
The position vector of the CM relative to C is:
$\vec{r}_{CM/C} = (X_{CM} - X_C)\hat{i} + (Y_{CM} - Y_C)\hat{j}$
$\vec{r}_{CM/C} = (L/4 - L/2)\hat{i} + (3h/4 - h/2)\hat{j}$
$\vec{r}_{CM/C} = (-L/4)\hat{i} + (h/4)\hat{j}$

The net torque about C due to the system's acceleration is:
$\vec{\tau}_{C, inertial} = \vec{r}_{CM/C} \times (M_{total} \vec{a}_{CM})$
$\vec{\tau}_{C, inertial} = [(-L/4)\hat{i} + (h/4)\hat{j}] \times (2M (-\mu g)\hat{i})$
$\vec{\tau}_{C, inertial} = (-L/4)( -2M\mu g)(\hat{i} \times \hat{i}) + (h/4)(-2M\mu g)(\hat{j} \times \hat{i})$
$\vec{\tau}_{C, inertial} = 0 + (h/4)(-2M\mu g)(-\hat{k})$
$\vec{\tau}_{C, inertial} = \frac{1}{2} M\mu gh \hat{k}$ (This is a counter-clockwise torque).

Now, let's calculate the net external torque about C due to the applied forces:

• Weight of the block ($Mg$): Acts at C. Torque is zero.
• Weight of particle A ($Mg$): Acts at $(0, h)$. Force is $-Mg\hat{j}$.
  Position vector from C to A is $\vec{r}_{A/C} = (0 - L/2)\hat{i} + (h - h/2)\hat{j} = -L/2\hat{i} + h/2\hat{j}$.
  $\vec{\tau}_{M_A g} = \vec{r}_{A/C} \times (-Mg\hat{j}) = (-L/2\hat{i} + h/2\hat{j}) \times (-Mg\hat{j})$
  $\vec{\tau}_{M_A g} = (-L/2)(-Mg)(\hat{i} \times \hat{j}) + (h/2)(-Mg)(\hat{j} \times \hat{j})$
  $\vec{\tau}_{M_A g} = (MgL/2)\hat{k}$ (Counter-clockwise).
• Normal reaction N: Acts at $(L/2, 0)$. Torque about C is zero, because its line of action passes through C's x-coordinate, and C is directly above it.
• Friction force $f_k$: Acts at $(L/2, 0)$. Force is $-f_k\hat{i} = -\mu N\hat{i}$.
  Position vector from C to the point of application of $f_k$ is $\vec{r}_{f_k/C} = (L/2 - L/2)\hat{i} + (0 - h/2)\hat{j} = -h/2\hat{j}$.
  $\vec{\tau}_{f_k} = \vec{r}_{f_k/C} \times (-\mu N\hat{i}) = (-h/2\hat{j}) \times (-\mu N\hat{i})$
  $\vec{\tau}_{f_k} = (-h/2)(-\mu N)(\hat{j} \times \hat{i})$
  $\vec{\tau}_{f_k} = (\mu N h/2)(-\hat{k}) = -\mu N h/2 \hat{k}$ (Clockwise).

The total external torque about C is:
$\vec{\tau}_{ext, C} = \vec{\tau}_{M_A g} + \vec{\tau}_{f_k} = (MgL/2)\hat{k} - (\mu N h/2)\hat{k}$
$\vec{\tau}_{ext, C} = (MgL/2 - \mu N h/2)\hat{k}$

Equating the external torque to the inertial torque:
$(MgL/2 - \mu N h/2)\hat{k} = (\frac{1}{2} M\mu gh)\hat{k}$
$MgL/2 - \mu N h/2 = \frac{1}{2} M\mu gh$

Substitute $N = 2Mg$:
$MgL/2 - \mu (2Mg) h/2 = \frac{1}{2} M\mu gh$
$MgL/2 - \mu Mgh = \frac{1}{2} M\mu gh$

Divide by $Mg$ (since $M, g \neq 0$):
$L/2 - \mu h = \frac{1}{2} \mu h$
$L/2 = \mu h + \frac{1}{2} \mu h$
$L/2 = \frac{3}{2} \mu h$

Now, substitute the given value of $\mu = \frac{2}{3}$:
$L/2 = \frac{3}{2} \left(\frac{2}{3}\right) h$
$L/2 = h$

So, the value of h in terms of L is $h = L/2$.

The final answer is $\boxed{L/2}$

Explanation of the solution:

1. Identify Masses and Total Mass: The block and particle A have equal mass M, so the total mass is 2M.
2. Calculate Normal Force: From vertical equilibrium, the normal force N equals the total weight, so $N = 2Mg$.
3. Calculate Acceleration: The only horizontal force is friction $f_k = \mu N$. This force causes the retardation. Using Newton's second law ($F_{net} = ma$), the acceleration is $a = \mu g$ (to the left).
4. Locate Center of Mass (CM): Calculate the coordinates of the CM of the combined system (block + particle A). With the origin at the bottom-left corner, $X_{CM} = L/4$ and $Y_{CM} = 3h/4$.
5. Apply Torque Equation about Geometrical Center (C): The problem states that the normal reaction passes through the geometrical center C of the block, which is at $(L/2, h/2)$. This implies the normal force and friction force act at $(L/2, 0)$ on the base.
   Since the system is accelerating but not rotating, the net external torque about any point P must be equal to $\vec{\tau}_P = \vec{r}_{CM/P} \times (M_{total} \vec{a}_{CM})$.
   • Calculate the inertial torque about C: $\vec{\tau}_{C, inertial} = ((-L/4)\hat{i} + (h/4)\hat{j}) \times (2M (-\mu g)\hat{i}) = \frac{1}{2} M\mu gh \hat{k}$.
   • Calculate the external torques about C:
     • Torque due to block's weight (at C): 0.
     • Torque due to particle A's weight (at $(0,h)$): $\vec{\tau}_{M_A g} = (MgL/2)\hat{k}$.
     • Torque due to normal force (at $(L/2,0)$): 0.
     • Torque due to friction force (at $(L/2,0)$): $\vec{\tau}_{f_k} = -\mu N h/2 \hat{k}$.
   • Sum the external torques: $\vec{\tau}_{ext, C} = (MgL/2 - \mu N h/2)\hat{k}$.
6. Equate Torques and Solve for h: Set $\vec{\tau}_{ext, C} = \vec{\tau}_{C, inertial}$ and substitute $N=2Mg$ and $\mu=2/3$.
   $MgL/2 - \mu (2Mg) h/2 = \frac{1}{2} M\mu gh$
   $L/2 - \mu h = \frac{1}{2} \mu h$
   $L/2 = \frac{3}{2} \mu h$
   $L/2 = \frac{3}{2} (\frac{2}{3}) h$
   $L/2 = h$

Answer:

The value of h is $L/2$.

Subject, Chapter and Topic:

Subject: Physics
Chapter: Systems of Particles and Rotational Motion
Topic: Dynamics of Rigid Bodies, Torque, Center of Mass, Rolling Motion (though here it's sliding, the principles of torque and CM are relevant).

Difficulty Level:

Medium

Question Type:

unknown