Question

A uniform plank leans against a cylindrical body of radius R as shown in figure, the right end B of the plank slides at a constant speed V to the right where as the cylindrical body moves at a constant speed of $V_0$ to the left side. The angular speed w of the rod at this instant, will be? distance between centre of cylinder and the end B is x. take V=15 m/s, $V_0$=5m/s, x = 5 m, R=3 m.

Answer 1

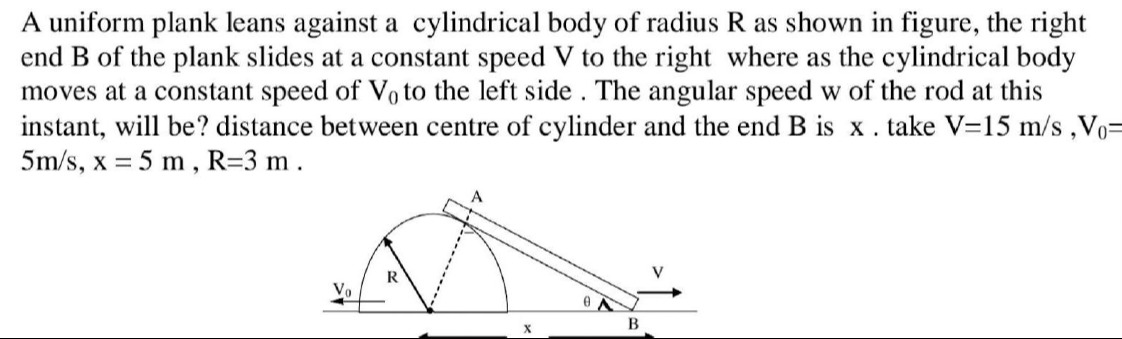
60

Answer 2

Let $\theta$ be the angle the plank makes with the horizontal. The angular speed of the plank is $\omega = -\frac{d\theta}{dt}$. Let the center of the cylinder be at $(x_c, R)$ and the end B of the plank be at $(x_B, 0)$. The cylinder moves to the left with speed $V_0$, so $\frac{dx_c}{dt} = -V_0$. The end B moves to the right with speed V, so $\frac{dx_B}{dt} = V$. The distance between the center of the cylinder and the end B is $x = x_B - x_c$. Differentiating with respect to time, $\frac{dx}{dt} = \frac{dx_B}{dt} - \frac{dx_c}{dt} = V - (-V_0) = V + V_0$.

The plank is tangent to the cylindrical body of radius R. Let the equation of the plank be $y = -\tan \theta (x - x_B)$. The distance from the center of the cylinder $(x_c, R)$ to the plank is R. The equation of the plank can be written as $x \tan \theta + y - x_B \tan \theta = 0$. The distance from $(x_c, R)$ to this line is $\frac{|x_c \tan \theta + R - x_B \tan \theta|}{\sqrt{\tan^2 \theta + 1}} = R$. $\frac{|R + (x_c - x_B) \tan \theta|}{\sec \theta} = R$. $|R - x \tan \theta| = R \sec \theta$. From the figure, the point of contact is above the horizontal line through the center of the cylinder and to the right of the vertical line through the center. Consider the triangle formed by the center of the cylinder C, the end B, and the point on the horizontal line through C at the x-coordinate of B. This is not helpful.

Let's consider the relationship between x, R, and $\theta$. Draw a perpendicular from the center of the cylinder C to the plank, meeting the plank at the point of tangency P. The length of CP is R. Let's consider the coordinates of the point of contact P. Let's consider the relative position of C with respect to the line containing the plank. The equation of the plank is $y = -\tan \theta (x - x_B)$. Consider the point $C' = (x_c, 0)$. The distance $C'B = x_B - x_c = x$. Consider the line segment CB. The angle the plank makes with the horizontal is $\theta$. Let's consider the distance from C to the plank. Draw a line through C parallel to the horizontal axis, and a line through B perpendicular to the horizontal axis. Let's consider the vertical distance from C to the horizontal ground, which is R. Let's consider the horizontal distance from C to B, which is x. Let's consider the relationship derived from the geometry: $R(1+\cos\theta) = x \sin\theta$.

We are given $R=3$, $x=5$. $3(1+\cos\theta) = 5 \sin\theta$. To find $\sin\theta$ and $\cos\theta$, we can try to solve this equation. $3 + 3\cos\theta = 5\sin\theta$. Square both sides: $(3 + 3\cos\theta)^2 = (5\sin\theta)^2$. $9 + 18\cos\theta + 9\cos^2\theta = 25\sin^2\theta = 25(1 - \cos^2\theta)$. $9 + 18\cos\theta + 9\cos^2\theta = 25 - 25\cos^2\theta$. $34\cos^2\theta + 18\cos\theta - 16 = 0$. $17\cos^2\theta + 9\cos\theta - 8 = 0$. Let $u = \cos\theta$. $17u^2 + 9u - 8 = 0$. Using the quadratic formula, $u = \frac{-9 \pm \sqrt{9^2 - 4(17)(-8)}}{2(17)} = \frac{-9 \pm \sqrt{81 + 544}}{34} = \frac{-9 \pm \sqrt{625}}{34} = \frac{-9 \pm 25}{34}$. Since $\theta$ is acute, $\cos\theta > 0$. So, $\cos\theta = \frac{-9 + 25}{34} = \frac{16}{34} = \frac{8}{17}$. Then $\sin\theta = \sqrt{1 - \cos^2\theta} = \sqrt{1 - (\frac{8}{17})^2} = \sqrt{1 - \frac{64}{289}} = \sqrt{\frac{289 - 64}{289}} = \sqrt{\frac{225}{289}} = \frac{15}{17}$. Check if $3(1+\cos\theta) = 5 \sin\theta$: $3(1 + \frac{8}{17}) = 3(\frac{17+8}{17}) = 3(\frac{25}{17}) = \frac{75}{17}$. $5 \sin\theta = 5(\frac{15}{17}) = \frac{75}{17}$. The relation holds.

Now differentiate $R(1+\cos\theta) = x \sin\theta$ with respect to time t. $R(-\sin\theta \frac{d\theta}{dt}) = \frac{dx}{dt} \sin\theta + x \cos\theta \frac{d\theta}{dt}$. $-R \sin\theta \omega = (V + V_0) \sin\theta - x \cos\theta \omega$. $x \cos\theta \omega - R \sin\theta \omega = (V + V_0) \sin\theta$. $\omega (x \cos\theta - R \sin\theta) = (V + V_0) \sin\theta$. $\omega = \frac{(V + V_0) \sin\theta}{x \cos\theta - R \sin\theta}$.

Substitute the given values: $V=15$, $V_0=5$, $x=5$, $R=3$. $\sin\theta = \frac{15}{17}$, $\cos\theta = \frac{8}{17}$. $V + V_0 = 15 + 5 = 20$. $x \cos\theta = 5 \times \frac{8}{17} = \frac{40}{17}$. $R \sin\theta = 3 \times \frac{15}{17} = \frac{45}{17}$. $x \cos\theta - R \sin\theta = \frac{40}{17} - \frac{45}{17} = -\frac{5}{17}$. $\omega = \frac{20 \times \frac{15}{17}}{-\frac{5}{17}} = \frac{20 \times 15}{-5} = -4 \times 15 = -60$. The angular speed is the magnitude, so $\omega = 60$ rad/s. The negative sign indicates that $\theta$ is decreasing, which means the plank is rotating clockwise.

Explanation of the solution:

1. Establish the relationship between the angle of the plank $\theta$, the distance x, and the radius R using the condition that the plank is tangent to the cylinder. The relationship is $R(1+\cos\theta) = x \sin\theta$.
2. Differentiate this relationship with respect to time, noting that $\frac{dx}{dt} = V + V_0$ and $\omega = -\frac{d\theta}{dt}$.
3. This gives an equation relating $\omega$, $\theta$, $x$, $R$, $V$, and $V_0$.
4. Use the given values of x and R to find $\sin\theta$ and $\cos\theta$ by solving the equation $R(1+\cos\theta) = x \sin\theta$.
5. Substitute the values of $V$, $V_0$, $x$, $R$, $\sin\theta$, and $\cos\theta$ into the differentiated equation to solve for $\omega$.