Question

A uniform metre scale is balanced at $60\,cm$ mark, when weight of $10\,gf$ and $30\,gf$ are suspended at $20\,cm$ mark and $90\,cm$ mark respectively. Calculate the weight of the metre scale ?

Answer 1

Since the metre scale has a constant density, the ruler's centre of gravity would be in the middle. According to the theory of moments, an object is in equilibrium if the number of anticlockwise moments about the same pivot equals the sum of clockwise moments.

Complete step by step answer:

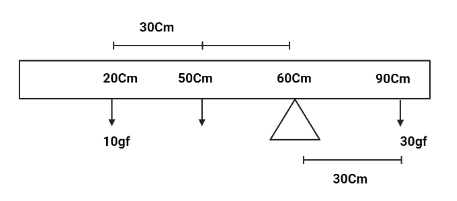
The mid-point of the meter scale is $50\,cm$ , let us denote this weight as $W$. Now, we know that two moments will act on the meter scale, that is clockwise and anticlockwise.

Let us first calculate clockwise moment:
The formula to calculate the clockwise moment is: Mass × Distance of the weight from pivot.
It is given in the question that $mass = 30$ and Distance of the weight from pivot $90 - 60 = 30\,cm$.
Substituting the values we get,
$30 \times 30 \\\ \Rightarrow 900gf.cm \\\$
Now, Let us calculate anticlockwise moment:
The formula to calculate the anticlockwise moment is: Mass × Distance of the weight from pivot.
It is given that there are two $mass = 10$ and $W$ and Distance of the weight from pivot $60 - 20 = 40cm$ and $60 - 50 = 10cm$ respectively
Substituting the values we get,
$10 \times 40 + W \times 10 \\\ \Rightarrow 400 + 10W \\\$
According to the principle of moment,
Anticlockwise moment =Clockwise moment.
$900 = 400 + 10W \\\ \Rightarrow 900 - 400 = 10W \\\ \Rightarrow 500 = 10W \\\ \therefore W = 50\,gf \\\$
Hence, the weight of the meter scale is $50\,gf$.

Note: A metre is a measurement unit that is used to determine the length of an object. A metre scale is used to determine the length of an item. A metre scale is graduated (or marked) in 100 centimetres, with each centimetre divided into ten millimetre divisions.