Question

A uniform meter scale is balanced horizontally on a knife edge at a distance of 10cm from its centre of gravity, when masses of 50g and 30g are suspended from the 5cm and 90cm marks of the rod. What is the weight of the meter scale?
A. 20 gram weight
B. 25 gram weight
C. 40 gram weight
D. 10 gram weight

Answer 1

The centre of gravity of 100cm meter scale will be at 50cm mark. Assume the meter scale is pivoted at the 40cm mark. Calculate the moment of forces around the centre of gravity. The net torque or moment of force on the system is zero since it is not rotating.

Formula used:
Torque, $\tau = F\,r$
where, F is the force and r is the distance from the origin to the action of force.

Complete step by step answer:
As we know the centre of gravity of 100cm meter scale will be at the 50cm mark. We have given that the meter scale is pivoted at 10cm from the centre of gravity. Therefore, let us assume the meter scale is pivoted at the 40cm mark on the meter scale as shown in the figure below.

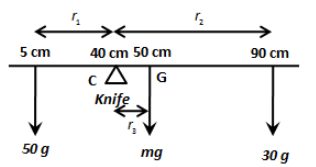
In the above figure, ${r_1}$ is the distance of mass of 50g from the pivot C, ${r_2}$ is the distance of mass 30g from C and ${r_3}$ is the distance of centre of gravity from C.

Suppose the moment of force at mark 5cm is anticlockwise then the moment of force at 50cm and 90cm marks are surely be clockwise.
Since the meter scale is not rotating, we can say that the net torque on the system is zero. Therefore,
${\tau _{net}} = 0$
$\Rightarrow - {\tau _1} + {\tau _2} + {\tau _3} = 0$
$\Rightarrow - 50g{r_1} + 30g{r_2} + mg{r_3} = 0$
$\Rightarrow 30g{r_2} + mg{r_3} = 50g{r_1}$
$\Rightarrow 30{r_2} + m{r_3} = 50{r_1}$
Substituting ${r_1} = 35\,{\text{cm}}$, ${r_2} = 50\,{\text{cm}}$ and ${r_3} = 10\,{\text{cm}}$ in the above equation, we get,
$30\left( {50} \right) + m\left( {10} \right) = 50\left( {35} \right)$
$\Rightarrow m\left( {10} \right) = 250$
$\therefore m = 25\,{\text{gm}}$
Therefore, the weight of the meter scale is 25 gram weight.

So, the correct answer is option B.

Note: You can assume the clockwise rotation of 50g weight and the result will be the same. To solve these types of questions, first thing that one should do is to determine the net torque. If the body is not rotating, the torque on the system is zero. We have assumed that the position of the pivot is towards the left of the centre of gravity. But you can assume it towards the right and the result remains the same.