Question

A uniform meter scale has two weights $10gf$ and $80gf$ suspended at the $10cm$ and marks respectively. If the meter scale itself weighs $50gf$ , find where must the weight be so that the meter scale stays balanced?

Answer 1

Hint : In the question, we are provided with a meter scale and we have to find the balanced point for the meter scale. By using the moments formula which states that moment is equal to the product of force and the perpendicular distance and then use the property that anticlockwise moment is equal to the clockwise moment.
$I = F \times d$

Complete Step By Step Answer:
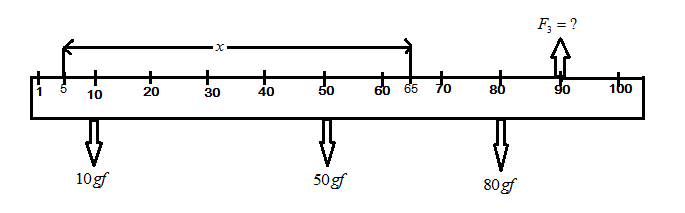
Let the equilibrium state for the meter scale be at point “x”. equilibrium state be defined as the balanced state.
Firstly, calculating the clockwise moment.
Clockwise moment about the point “x” = moment about $80gf$
$= 80gf \times \left( {80 - x} \right)cm$ $\ldots \left( 1 \right)$
Now, calculating the anticlockwise moment.
Anticlockwise moment about the point “x” = moment about $10gf$ + moment about $50gf$
$= 10gf \times \left( {x - 10} \right)cm + 50gf \times \left( {x - 50} \right)cm$ $\ldots \left( 2 \right)$
Using the property that at the equilibrium point anticlockwise moment is equal to the clockwise moment.
Equating the above two marked equations,
$80gf \times \left( {80 - x} \right)cm = 10gf \times \left( {x - 10} \right)cm + 50gf \times \left( {x - 50} \right)cm \\\ 6400 - 80x = 10x - 100 + 50x - 2500 \\\ 140x = 9000 \\\ \Rightarrow x = \dfrac{{9000}}{{140}} = 64.285cm \\\$
Hence, the balanced point is $64.28cm$ from the beginning.

Note :
Moments represent a very short interval of time. Moment of force formula is applicable for the balanced as well as unbalanced forces. Keep in mind here we are using the perpendicular distance. Be careful about writing the units.