Question

A uniform meter scale balances horizontally on a knife-edge placed at $55cm$ mark, when a mass of $25g$ is supported from one end, then the mass of the scale is:
$A)200g$
$B)225g$
$C)350g$
$D)275g$

Answer 1

According to the principle of moments, the clockwise moment of a scale, balanced on a pivot, is equal to the anticlockwise moment of the scale. If a uniform meter scale is balanced on a pivot, located at the centre of the scale, the total mass of the scale is said to be resting on this pivotal point, at the centre of the scale. To solve the given problem, we need to apply the principle of moments to the right arm of the given uniform meter scale. We proceed by considering that the right arm of the scale is balanced on a knife edge.
Formula used:
$1){{I}_{1}}={{m}_{1}}{{l}_{1}}$
$2){{I}_{2}}={{m}_{2}}{{l}_{2}}$
$3){{I}_{1}}={{I}_{2}}\Rightarrow {{m}_{1}}{{l}_{1}}={{m}_{2}}{{l}_{2}}$

Complete answer:
According to the principle of moments, a body is said to be in equilibrium if the algebraic sum of all the moments acting on that body about the axis of rotation is equal to zero. Thus, if a uniform meter scale is balanced on a pivot using two different masses on both of its ends, the total sum of clockwise moments acting through the right arm of the scale $(BC)$ is equal to the total sum of anticlockwise moments acting through the left arm of the scale$(AB)$, as shown in the following figure.

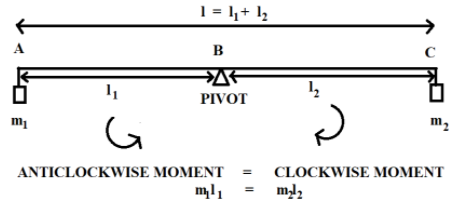
Clockwise moment of a scale is equal to the product of mass suspended on the right end of the scale and the length between the right end and the pivot of the scale. It acts in clockwise direction as shown in the figure given above. Similarly, an anticlockwise moment of a scale is equal to the product of mass suspended on the left end of the scale and the length between the left end and the pivot of the scale. It acts in anticlockwise direction as shown in the figure given above. Pivot of a scale is nothing but the point at which a scale is balanced using two different masses. If two equal masses are used to balance a uniform meter scale, the pivot of the scale is exactly at the midpoint of the scale, at the$50cm$, from both ends of the scale.
Mathematically, if ${{I}_{1}}$ represents the anticlockwise moment of a scale, it is given by
${{I}_{1}}={{m}_{1}}{{l}_{1}}$
where
${{I}_{1}}$ is the anticlockwise moment of a scale
${{m}_{1}}$ is the mass suspended on the left end of the scale
${{l}_{1}}$ is the length between the left end and the pivot of the scale
Let this be equation 1.
Similarly, if ${{I}_{2}}$ represents the clockwise moment of a scale, it is given by
${{I}_{2}}={{m}_{2}}{{l}_{2}}$
where
${{I}_{2}}$ is the clockwise moment of a scale
${{m}_{2}}$ is the mass suspended on the right end of the scale
${{l}_{2}}$ is the length between the right end and the pivot of the scale
Let this be equation 2.
According to the principle of moments, equation 1 is equal to equation 2. Thus, we have
${{I}_{1}}={{I}_{2}}\Rightarrow {{m}_{1}}{{l}_{1}}={{m}_{2}}{{l}_{2}}$
Let this be equation 3.

Now, let us consider a uniform meter scale of $100cm$ balancing horizontally on a knife-edge, placed at $55cm$, from the left end of the scale, as shown in the following figure.

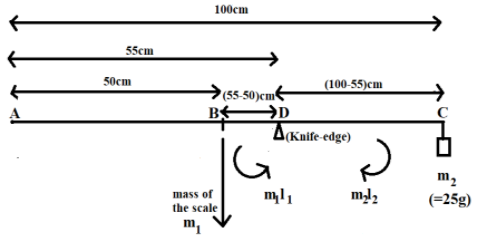
From the figure, it is clear that the left end of the scale is denoted by point $A$ and the right end of the scale is denoted by point $C$. The scale balances on a knife-edge, placed at a distance of $55cm$ from the left end of the scale, at point $D$. Also, a mass of $25g$ is supported from the right end of the scale, at point $C$. We are required to find the mass of the scale from this setup.
We know that the mass of a uniform meter scale rests on its pivotal point, at a distance of $50cm$, from both ends of the scale. In the given figure, the pivot of the uniform meter scale is denoted by point $B$, at a distance of $50cm$, from both $A$ and $C$. Now, if we apply the principle of moments to the right arm of the scale (denoted by $BC$) with the knife-edge at point $D$ as the pivot of the right arm, we can easily calculate the mass of the scale. The right end of $BC$ supports a mass of $25g$ whereas the left end of $BC$ can be considered to support the mass of the scale.
According to the principle of moments, the clockwise moment of $BC$ is equal to the anticlockwise moment of $BC$.
From equation 1, anticlockwise moment of $BC$ is given by
${{I}_{1}}={{m}_{1}}{{l}_{1}}={{m}_{1}}\times (55cm-50cm)={{m}_{1}}\times 5cm$
where
${{I}_{1}}$ is the anticlockwise moment of the right arm of the scale ($BC$)
${{m}_{1}}$ is the mass of the scale
${{l}_{1}}=(55cm-50cm)=5cm$, is the length between $B$ and $D$
Let this be equation 4.
Similarly, from equation 2, clockwise moment of $BC$ is given by
${{I}_{2}}={{m}_{2}}{{l}_{2}}=25g\times (100cm-55cm)=25g\times 45cm=1125gcm$
where
${{I}_{2}}$ is the clockwise moment of the right arm of the scale ($BC$)
${{m}_{2}}=25g$, is the mass suspended on the right end of the scale
${{l}_{2}}=(100cm-55cm)=45cm$, is the length between $C$ and $D$
Let this be equation 5.
Substitution equation 4 and equation 5 in equation 3, we have
${{I}_{1}}={{I}_{2}}\Rightarrow {{m}_{1}}{{l}_{1}}={{m}_{2}}{{l}_{2}}\Rightarrow {{m}_{1}}\times 5cm=1125gcm\Rightarrow {{m}_{1}}=\dfrac{1125gcm}{5cm}=225g$
Therefore, the mass of the scale is equal to $225g$.

The correct option to be marked is $B$.

Note:
Students might wonder why the principle of moments is applied to the right arm of the uniform meter scale. This is because we are asked to find the mass of the scale and not the mass suspended to the extreme left end of the scale. Mass of a uniform meter scale rests on the pivot of the scale, at the midpoint of the scale. Therefore, it is enough to apply the principle of moments to the right arm of the scale, with the knife-edge as the new pivot of the right arm of the scale. In this way, we tend to ignore the left arm of the meter scale.