Question

A uniform metallic wire has a resistance of 18 Ω and is bent into an equilateral triangle. Then, the resistance between any two vertices of the triangle is
(A) $8\Omega$
(B) $12\Omega$
(C) $4\Omega$
(D) $2\Omega$

Answer 1

Hint
When we bend the wire into an equilateral triangle, then the resistance divides equally into three parts for the three equal sides. We need to calculate the division resistance divided and find the equivalent resistance of the whole combination.
Formula used: In this question, we will be using the following formula,
${R_{eq}} = {R_1} + {R_2} + {R_3} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in series.
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in a parallel circuit.

Complete step by step answer
Let us consider the two vertices of the triangle as A and B.
When we bend the metallic wire into an equilateral triangle, we get the figure as,

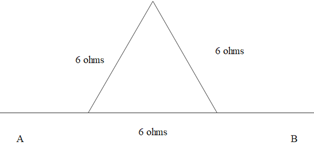
So when we bend the wire into three equal parts, the resistance of the metallic wire is divided equally for the three sides of the triangle. Now, when we try to simplify the diagram to see the combination of the resistances, we get a figure as,

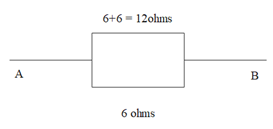
In the top wire, the resistances are in series, so we can calculate the total resistance using the formula ${R_{eq}} = {R_1} + {R_2} + {R_3} + ....$
We can substitute, ${R_1} = {R_2} = 6\Omega$
Hence we get
${R_{eq1}} = 6 + 6 = 12\Omega$
Now, we see that the base of the triangle has 6 ohms resistance and it is parallel to the above side.
Then we can use the formula, $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$
Substituting ${R_1} = 6\Omega$ and ${R_2} = {R_{eq}} = 12\Omega$ we get
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{6} + \dfrac{1}{{12}}$
Taking LCM as 12
$\dfrac{1}{{{R_{eq}}}} = \dfrac{{2 + 1}}{{12}} = \dfrac{1}{4}$
On taking reciprocal we get,
${R_{eq}} = 4\Omega$
Thus, the resistance between the two vertices A and B is 4 ohms.
Hence, the correct answer is option (C).

Note
The resistance of a wire depends on the resistivity of the material, the length of the wire and the area of the cross section. Here the wire is bending into three equal parts. So considering the area of the cross section to be the same everywhere, we have considered the resistance gets divided into three equal parts.