Question

A uniform metal disc of radius $R$ is taken and out of it a disc of diameter $\dfrac{R}{2}$ is cut off from the end. The center of mass of the remaining part will be:
(A) $\dfrac{R}{{10}}$ from the center
(B) $\dfrac{R}{{15}}$ from the center
(C) $\dfrac{R}{5}$ from the center
(D) $\dfrac{R}{{20}}$ from the center

Answer 1

First we have to draw a rough diagram showing the required parameters to solve the problem. From the above given condition we can say that the density of the disc will be uniform. Now we will geometrically compare the dimension in both the cases. We will get the area now using the center of mass along the x coordinate we will get the center of mass of the remaining part.

Complete step by step answer:
As per the problem we have a uniform metal disc of radius $R$ is taken and out of it a disc of diameter $\dfrac{R}{2}$ is cut off from the end.
We need to calculate the center of mass of the remaining part.

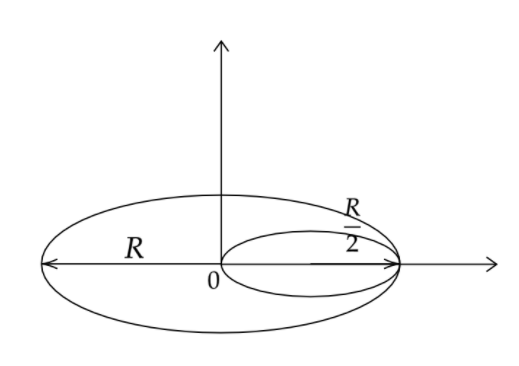
The density of the disc will remain uniform all over the surface, so now we can use a geometrical method to find their area.
Area of the larger disc,
${A_1} = \pi {R^2}$
Now the area of the cutoff disc is,
${A_2} = \pi {\left( {\dfrac{R}{4}} \right)^2} = \dfrac{{\pi {R^2}}}{{16}}$
Calculating the center of mass of the remaining potion across the x coordinate we will get,
${X_{COM}} = \dfrac{{{A_1}{X_1} - {A_2}{X_2}}}{{{A_1} - {A_2}}}$
Here,
${A_1}$ is the area of the larger disc of radius $R$.
${A_2}$ is the area of the removed disc of radius $\dfrac{R}{4}$.
${X_1}$ is the distance of center of mass of the larger disc from the ${X_{COM}}$.
${X_2}$ is the distance of center mass of the smaller disc from the ${X_{COM}}$.
Now putting the respective values in the above formula we will get,
${X_{COM}} = \dfrac{{\pi {R^2}\left( 0 \right) - \dfrac{{\pi {R^2}}}{{16}}\left( {\dfrac{{3R}}{4}} \right)}}{{\pi {R^2} - \dfrac{{\pi {R^2}}}{{16}}}}$
$\Rightarrow {X_{COM}} = \dfrac{{ - \left( {\dfrac{{3{R^3}}}{{64}}} \right)}}{{\dfrac{{15{R^2}}}{{16}}}}$
Cancelling the common terms we will get,
${X_{COM}} = - \dfrac{R}{{20}}$
Hence the center of mass is at $\dfrac{R}{{20}}$ from the center.
Therefore the correct option is (D).

Note: Center of mass is a position that defines the relative to an object or system of objects. The distribution of mass in space is the unique point where the weighted relative position of the distributed mass sums to zero. Keep in mind that center of mass is the point to which force may be applied to cause a linear acceleration without any angular acceleration.