Question

A uniform metal disc of radius $R$ is taken and out of it. A disc of diameter $R$ is cut off from the end. The centre of mass of the remaining part will be ?

Answer 1

Hint : Product of center of mass and area of the remaining part of the disc is equal to that of the cut out part. After substitution of every known value and the variable denoting the center of mass of the remaining part of the disc, we will be able to determine the latter.
Product of center of mass and area: ${x_1}{A_1} = {x_2}{A_2}$
Where ${x_1},{x_2}$ are the distance of the center of masses of remaining part and cut out part of the disc from the center of the original disc and is expressed in meter $(m)$ and ${A_1},{A_2}$ are the areas of the of remaining part and cut out part of the disc and is expressed in meter square $({m^2})$ .

Complete Step By Step Answer:
We have the following information from the given question:
Radius of original disc $= R$
Diameter of the cut out disc $= R$ . Therefore, radius of the cut out disc $= R/2$
Let,
${C_1},{C_2}$ be the center of masses of the remaining part and cut out part of the disc and $O$ be the center of the original disc.
Therefore, we have the distance of the center of masses of the remaining part and cut out part of the disc from the center of the original disc as .
That is, and $O \to {C_2} = R/2m = {x_2}(say)$ .
The diagrammatic representation will be as follows:

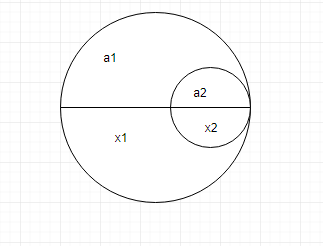
We know that the equation for center of mass of disc segments is ${x_1}{A_1} = {x_2}{A_2}$ .
Substituting the values of the ${x_1},{x_2}$ in the above we get,
${x_1}{A_1} = {x_2}{A_2} \\\ \Rightarrow x{A_1} = R/2{A_2} \\\$
But,
${A_1} =\text{ area original disc }- \text{area of cutout part} = \pi {R^2} - \pi {(\dfrac{R}{2})^2} \\\ \Rightarrow {A_1} = \pi {R^2} - \pi {(\dfrac{R}{2})^2} \\\$ and
${A_2} = \pi {(\dfrac{R}{2})^2}$
Substituting we get,
$x{A_1} = R/2{A_2} \\\ \Rightarrow x \times \pi {R^2} - \pi {(\dfrac{R}{2})^2} = R/2 \times \pi {(\dfrac{R}{2})^2} \\\$
Upon simplification we get,
$x \times \pi {R^2} - \pi {(\dfrac{R}{2})^2} = R/2 \times \pi {(\dfrac{R}{2})^2} \\\ \Rightarrow x \times \pi {R^2} - {(\dfrac{R}{2})^2} = R/2 \times {(\dfrac{R}{2})^2} \\\ \Rightarrow x(\dfrac{3}{4}{R^2}) = \dfrac{R}{2}(\dfrac{{{R^2}}}{4}) \\\ \Rightarrow x3 = \dfrac{R}{2} \\\ \Rightarrow x = \dfrac{R}{6}m \\\$
Therefore, The centre of mass of the remaining part will be $\dfrac{R}{6}m$ .

Note :
The center of mass’s distance of new segments of a disc are always calculated from the center of the original disc. They might be equal to another segment but never equal to that of the original disc. Therefore, the distance of the center of mass must be chosen carefully.