Question
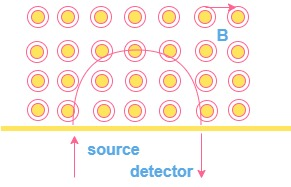
Question: A uniform magnetic field with a slit system shown in fig. is to be used as a momentum filter for hig...
A uniform magnetic field with a slit system shown in fig. is to be used as a momentum filter for high energy charged particles. With a field B tesla, it is found that the filter transmits α -particles each of energy 5⋅3 MeV. The magnetic field is increased to 2⋅3 B Tesla and deuterons are passed into the filter. The energy of each deuteron transmitted by the filter is…
(A) 5MeV
(B) 7MeV
(C) 14MeV
(D) 21MeV
Solution
Hint : The centripetal force required by the ion to move in a circular path is provided by the perpendicular magnetic field B.
qvB=rmv2
m is mass of charge particle to be accelerated, B is magnetic field, q is charge on particle, v is velocity of charge particle, r is radius of circular path.
The energy of particle is given E=2mp2
p is the momentum of a particle.
Using the above formulas we will get the required result.
Complete step by step solution:
We have given, high energy charge particle in the magnetic field B Tesla.
Radius of charge particle is given by,
r=qBmv=qBP∴r=Bq2Em
Radius in case of α -particles
rα=Bqα2Eαmα
Radius in case of deuteron –particle is given by
rd=2.3Bqd2Edmd
Since the radius for both the particle is same
Bqα2Eαmα=2⋅3Bqd2Edmd
Squaring on both sides
qα22Eαmα=(2⋅3)2qd22Edmd ---- (1)
Since,
qαqd=2ee=21
qd is charge on deuteron, qα is charge on α -particle
mdmα=24=2
mα is mass of α -particle, md is mass of deuteron
Eα (energy of α -particle = 5.3 MeV
Put all in eq. (1)
(2.3)2×(qαqd)2mdEαmα=Ed(2.3)2×(21)2×5.3MeV(2)=Ed
Energy of deuteron particle is given by,
Ed=4(2.3)2×2×5.3MeVEd=14.01MeV .
Note:
Motion of charge particle in magnetic field explained below:
Then the centripetal force acquired by charged particle to move in circular path is provided by perpendicular magnetic field B is given by
Fe=rmv2 --- (1)
Fb=qvB --- (2)
From eq (1) and (2)
rmv2=qvBrmv=Bq
r=qBmv This is the radius of circular path.
The momentum of particle is given
P=mv
And energy of particle is,
E=2mP2
Or
P=2mE ,
Radius of charge particle is given by
r=qBmv=qBP∴r=Bq2Em.
