Question

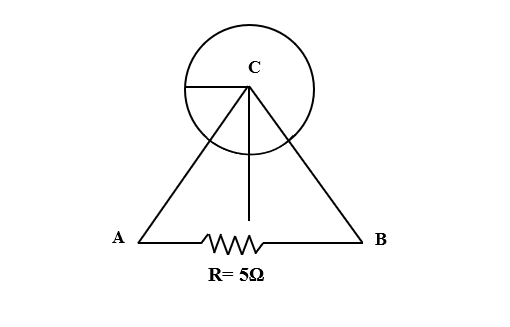
A uniform magnetic field of intensity $B={B}_{0} \sin (\omega t)$ directed into the plane of the paper exists in the cylindrical region of radius r. A loop of resistance $R= 5 \Omega$ is folded in the form of an equilateral triangle of side length 2r is placed as shown in the figure. The maximum potential drop in the wire AB is

A. $\dfrac {\pi {r}^{2}{B}_{0}\omega}{6}volt$
B. $\dfrac {\pi {r}^{2}{B}_{0}\omega}{3}volt$
C. $\dfrac {\pi {r}^{2}{B}_{0}\omega}{2}volt$
D. $\pi {r}^{2}{B}_{0}\omega$

Answer 1

To solve this problem, use the relationship between magnetic flux, magnetic field and area. Find the area of the cylindrical region. Substitute the area and magnetic field in the formula for magnetic flux. Then, integrate the obtained equation. For potential drop to be maximum, use the condition $\cos {\omega t}= 1$. Substitute this condition and find the maximum potential drop in the wire AB.
Formula used:
$\phi= BA$

Complete answer:
Given: R= $5 \Omega$
Length of side of triangle (l)= 2r
The given triangle is an equilateral triangle. Hence, each angle is 60°.
$\Rightarrow \angle ABC= \angle BCA= \angle CAB= 60°$
Magnetic flux is given by,
$\phi= BA$ …(1)
Where, B is the magnetic field
A is the area perpendicular to the magnetic field B
Area of the cylindrical region is given by,
$A= \pi {r}^{2} \times \dfrac {60°}{360°}$
$\Rightarrow A= \dfrac {\pi {r}^{2}}{6}$ …(2)
Magnetic field is given by,
$B={B}_{0} \sin (\omega t)$
Substituting equation. (2) in equation. (1) we get,
$\phi= {B}_{0} \sin (\omega t) \times \dfrac {\pi {r}^{2}}{6}$ …(3)
Integrating equation. (3) with respect to time we get,
$\dfrac {d\phi}{dt}= {B}_{0}\omega \cos (\omega t) \times \dfrac {\pi {r}^{2}}{6}$ …(4)
The potential drop will be maximum at $\omega t=0°$.
Substituting this in the equation. (4) we get,
$\dfrac {d\phi}{dt}= {B}_{0}\omega \cos {0°} \times \dfrac {\pi {r}^{2}}{6}$
$\Rightarrow \dfrac {d\phi}{dt}= {B}_{0}\dfrac {\pi {r}^{2}}{6}$
Hence, the maximum potential drop in the wire AB is $\dfrac {\pi {r}^{2}{B}_{0}\omega}{6}volt$.

So, the correct answer is option A i.e. $\dfrac {\pi {r}^{2}{B}_{0}\omega}{6}volt$.

Note:
Students must remember the condition for maximum potential drop and minimum potential drop. For maximum potential drop we consider $\omega t=0°$. While for minimum potential drop, we consider $\omega t=90°$. But students should keep in mind that at $\omega t=90°$, we get the lowest absolute value. As the magnetic flux can also have a negative value.