Question

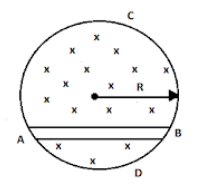
A uniform magnetic field of induction B fills a cylindrical volume of radius R. A rod AB of length $2l$ is placed as shown in figure. If B is changing at the rate $\dfrac{{dB}}{{dt}}$ , the emf that is produced by the changing magnetic field and that acts between the ends of the rod is

Answer 1

Hint : Here we have to first draw a triangle from O to AB , then find the area of this triangle and as we know that the emf induced is equal to the area multiplied by the time rate of change of magnetic field, thus, we can find the value of the between the ends of the rods.
The formula for the emf induced is given by
$\varepsilon = A \dfrac{dB}{dt}$
Where $A$ is the area of the rod and $\dfrac{{dB}}{{dt}}$ is the time rate of change of magnetic field.
Area of triangle= $\dfrac{1}{2} \times base \times height$ .

Complete Step By Step Answer:
The formula for the emf induced is given by
$\varepsilon = A \dfrac{dB}{dt}$
Where $A$ is the area of the rod
Consider the triangle $OAB$ formed by the point $O$ and the rod $AB$
The area of the triangle is
$A = \dfrac{1}{2} \times 2l \times OC = l \times OC$
Now
OC = \sqrt {O{B^2} - B{C^2}} \\\ \Rightarrow OC = \sqrt {{R^2} - {l^2}} \\\
Therefore, $A = l\sqrt {{R^2} - {l^2}}$
Thus, the emf induced between the ends of the rod $AB$ is $\varepsilon = \dfrac{{dB}}{{dt}}l\sqrt {{R^2} - {l^2}}$ .

Note :
The induced emf of this conductor depends on the change of flux through this sphere which further depends on the change of magnetic field through the area of the triangle. The area of the triangle is taken and not just for the rod as the flux is the same for the whole area around the rod.