Question
Question: A uniform magnetic field of induction \(B\) fills a cylindrical volume of radius \(R\). A rod \(AB\)...
A uniform magnetic field of induction B fills a cylindrical volume of radius R. A rod AB of length 2l is placed as shown in figure. If B is changing at the rate dB/dt, the emf that is produced by the changing magnetic field and that acts between the ends of the rod is
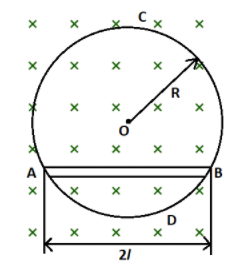
A.dtdBlR2−l2B.dtdBlR2+l2C.21dtdBlR2−l2D.21dtdBlR2+l2
Solution
Consider a concentric circle smaller than the given one, which is tangent to line AB. Then find the electric field from that circle, which will help in getting the emf that is produced in the changing magnetic field.
Formula used:
EMF(ε)=∫Edl
Complete step by step answer:
Consider a point on the circumference of a circle of radius r(r<R), which is concentric to the bigger circle. Let, E be the electric field along the tangents to the circle.
Then, E is given by,
E=2rdtdB
Now,
Consider a point P in the rod and a small distance dt, which is along AB.
So, dt=PQalongAB
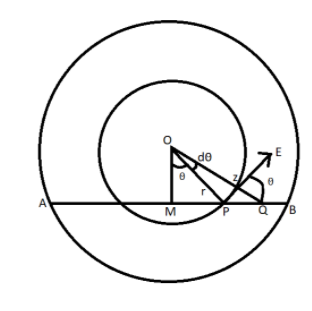
Hence,
EMF(ε)=∫Edl
where, E=2rdtdB and dl=dlcosθ
Then,
