Question

A uniform ladder of length $10.0m$ and mass $16.0kg$ is resting against a vertical wall making an angle of ${37^ \circ }$ with it. The vertical wall is frictionless but the ground is rough. An electrician weighing $60.0kg$ climbs up the ladder. If he stays on the ladder at a point $8.00m$ from the lower end, what will be the normal force and the force of friction on the ladder by the ground? What should be the minimum of friction for the electrician to work safely?

Answer 1

The ladder and electrician system should be in equilibrium to ensure that the man can work safely. We construct a free body diagram, depicting the forces and their directions.

Complete step by step answer:
It has been given that a uniform ladder of length $10.0m$ and mass $16.0kg$ is resting against a vertical wall making an angle of ${37^ \circ }$ with it. The vertical wall is frictionless but the ground is rough. An electrician weighing $60.0kg$ climbs up the ladder. He stays on the ladder at a point $8.00m$ from the lower end.
It must be remembered that the ladder and electrician system should be in equilibrium to ensure that the man can work safely.
We construct a free body diagram, depicting the directions of forces. The diagram has been given below.

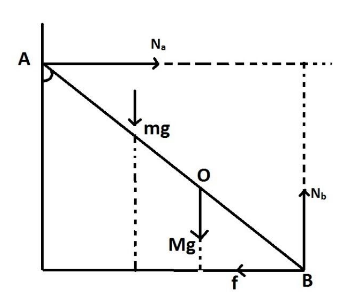
Here A is the vertical axis and represents the vertical wall on which the ladder rests. The line AB depicts the ladder and point O marks the point where the weight of the ladder acts downwards towards the ground while the point where the man is at 8m above the ground is marked by an arrow $mg$ .
For equilibrium $\sum {F = 0}$ and $\sum \tau = 0$ where $F$ is the force and $\tau$ is the torque.
We divide the force into two components, one along the horizontal x-axis represented by ${F_x}$ and the other along the vertical y-axis, represented by ${F_y}$ .
For, $\sum {{F_x} = 0}$ , the forces acting in the horizontal direction must thus be equal.
The horizontal forces acting are, the normal reaction force of the wall, that is represented by ${N_a}$ and the force of friction between the ladder and the ground, that is represented by, $f$ .
${N_a} = f$
For $\sum {{F_y} = 0}$ , the forces acting in the vertical direction must thus be equal.
Now the forces acting in the vertical direction are, ${N_b}$ , that is, the normal reaction force of the ladder, $mg$ , the weight of the man, and $Mg$ , the weight of the ladder.
Thus, mathematically, ${N_b} = mg + Mg$ .
Now, we have, $m = 60kg$ , $M = 16kg$ and $g = 10m{s^{ - 2}}$ .
Substituting these values we get,
${N_b} = mg + Mg = 60 \times 10 + 16 \times 10$
$\Rightarrow {N_b} = 760N$
Torque is the measure of the force that can cause an object to rotate about an axis. Force is what causes an object to accelerate in linear kinematics. Similarly, torque is what causes an angular acceleration. Hence, torque can be defined as the rotational equivalent of linear force. The point where the object rotates is called the axis of rotation. In physics, torque is simply the tendency of a force to turn or twist.
Mathematically torque about a point is given by, $\tau = F \cdot r\sin \theta$ whereas $F$ is the magnitude of force, $r$ is the perpendicular distance between the point about which torque is calculated and the point of application of force and $\theta$ is the angle between the direction of application of force and the direction of $r$ .
Taking torque about B,
${N_a}10\cos {37^ \circ } = mg.8\sin {37^ \circ } + Mg5\sin {37^ \circ }$
${N_a} = \dfrac{{\tan {{37}^ \circ }}}{{10}}\left( {65 \times 10 \times 8 + 16 \times 10 \times 5} \right)$
From the calculations above and the given question, $f = {N_a} = 420N$ .
Coefficient of friction, ratio of the frictional force resisting the motion of two surfaces in contact to the normal force pressing the two surfaces together.
For maximum value of coefficient of friction, $f \leqslant \mu {N_b}$
$\mu \geqslant \dfrac{f}{{{N_b}}}$
Thus, $\dfrac{f}{{{N_b}}} = \dfrac{{420}}{{760}} = 0.55$ .
Hence, the minimum of friction for the electrician to work safely is $0.55$ .

Note:
Since, the ladder should not slip or rotate, the total torque is zero. The value we have achieved here is solely based on the assumption that, $g = 10m{s^{ - 2}}$ . Please note that, the value of the coefficient of kinetic friction ${\mu _k}$ may change if the acceleration due to gravity is taken to be, $g = 9.8m{s^{ - 2}}$ . In that case, the calculations need to be changed while the procedure remains the same.