Question

A uniform horizontal meter scale of mass m is suspended by two vertical strings attached to its two ends. A block of mass 3m is placed on the 60cm mark. The tensions in the two strings are in the ratio.
A). 17:19
B). 19:21
C). 17:23
D). 19:23

Answer 1

The term tension, In terms of string, it is described by the force exerted by a string when it is subjected to pull. If a person is holding a block of weight W attached to the end of a string, a force is experienced by the person.

Complete step by step solution:
According to the question.
In this Diagram it is clear it is in equilibrium.

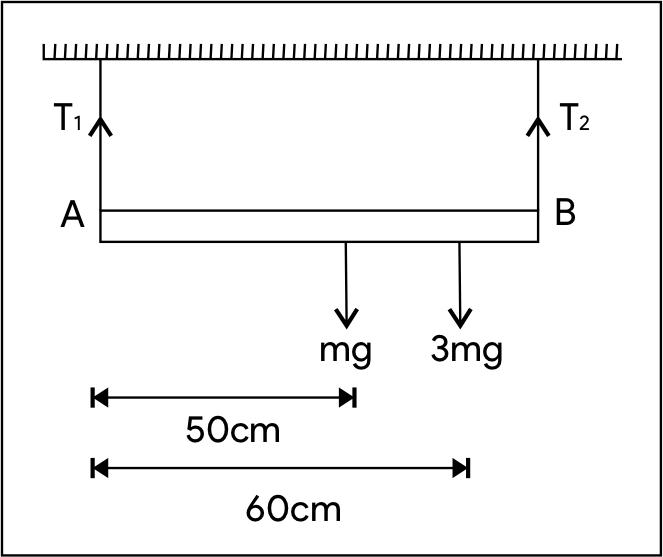
The condition of the equilibrium is that the net force on the body is zero and the net torque on the body is zero. Means
$\sum F = 0 \\\ and \\\ \sum \tau = 0 \\\$
So, in this diagram we see that there is no force on the horizontal side. And there is a force on the vertical side. So, the forces are balanced.
Then we apply the condition of the equilibrium, for the net force is zero.
So, the sum of tensions is:
${T_1} + {T_2} = mg + 3mg$
So, ${T_1} + {T_2} = 4mg$ -- (A)
Here, $T_1$ is the tension on the 1st string
$T_2$ is the tension on the 2nd string
m is the mass
g is the acceleration due to gravity
Then we apply the condition of the equilibrium, for the net torque is zero.
Now, torque at the middle point of the meter scale is zero because there are no rotational motions.
So, the torque due to end A + torque due to meter scale +torque due to block +torque due to end B=0
So, the
${T_1} \times 50cm(clockwise) + mg \times 0 + 3mg \times 10(clockwise) + {T_2} \times 50cm(anticlockwise) = 0$
Now, solving
$50{T_1} + 30mg - 50{T_2} = 0$
$\Rightarrow 5{T_1} + 3mg + ( - 5{T_2}) = 0$
$\Rightarrow 5{T_2} - 5{T_1} = 3mg$--- (B)
Multiply by equation (A) from 3 and equation (B) from 4
$3{T_1} + 3{T_2} = 12mg$ --- (C)
$\Rightarrow 20{T_2} - 20{T_1} = 12mg$ --- (D)
Now, equate
$\begin{aligned} & 3{T_1} + 3{T_2} = 20{T_2} - 20{T_1} \\\ & \Rightarrow 23{T_1} = 17{T_2} \\\ & \Rightarrow \dfrac{{{T_2}}}{{{T_1}}} = \dfrac{{17}}{{23}} \\\ \end{aligned}$
So, the option (C) is correct.

Note: We know that the pressure is the physical force exerted on an object. The force applied is perpendicular to the surface of the objects. We need to be focused on the direction of forces for finding the correct torque.