Question

A uniform heavy rod of length L, weight W and cross-sectional area A is hanging from a fixed support. Young’s modulus of the material is Y. Find the elongation of the rod.

${\text{A}}{\text{. }}\dfrac{{WL}}{{AY}} \\\ {\text{B}}{\text{. }}\dfrac{{WL}}{{2AY}} \\\ {\text{C}}{\text{. }}\dfrac{{WL}}{{4AY}} \\\ {\text{D}}{\text{. }}\dfrac{{WL}}{{3AY}} \\\$

Answer 1

Hint: When a material is subjected to stress and strain, elongation may take place in the material which depends on the Young’s modulus of that material. Young’s modulus is defined as the ratio of stress to strain.

Complete step by step answer:
Young’s modulus of a material is defined as the ratio of stress to the strain for that material. It basically tells us how a material will elongate when subjected to stress. It is also called modulus of elasticity or tensile modulus. It is the slope of the graph between stress and strain.
Elongation in material is equal to the ratio of change in length to the total length of the material.
$\Delta l = \dfrac{{\Delta x}}{x}$
We have a rod of total length L. Consider a small element dx at a distance of x from the top. Its distance from the bottom is L-x. Diagrammatically, we can represent it as follows:

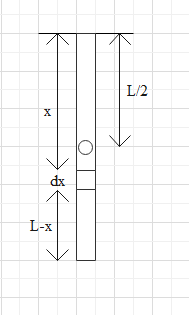
The weight of the part below this element is equal to W’ which is given as the product of total weight of rod W and the ratio of length hanging below x to the total length of the rod L.
$W' = W \times \dfrac{{L - x}}{L}$
If dl is the elongation in the element dx then young’s modulus is given as
$Y = \dfrac{{Stress}}{{Strain}} = \dfrac{{\dfrac{F}{A}}}{{\dfrac{{dl}}{l}}} = \dfrac{{Fl}}{{Adl}}$
Here $F = W',l = dx$ for small element and elongation is given as
$dl = \dfrac{{W'}}{{AY}}dx$
Integrating both sides we get
Elongation $l = \int {\dfrac{{W'}}{{AY}}dx}$
Since cross-sectional area A and Young’s modulus Y are constants. They can be taken outside of the integral.
$\therefore l = \dfrac{1}{{AY}}\int {W'dx} \\\ \\\$
Putting various values, we get
$l = \dfrac{W}{{AYL}}\int\limits_0^L {\left( {L - x} \right)} dx \\\ \Rightarrow l = \dfrac{W}{{AYL}}\left( {Lx - \dfrac{{{x^2}}}{2}} \right)_0^L \\\ \Rightarrow l = \dfrac{W}{{AYL}}\left( {{L^2} - \dfrac{{{L^2}}}{2} - 0} \right) \\\ \Rightarrow l = \dfrac{W}{{AYL}} \times \dfrac{{{L^2}}}{2} \\\ \Rightarrow l = \dfrac{{WL}}{{2AY}} \\\$
Hence, the correct answer is option B.

Note: Elongation is inversely proportional to the Young’s modulus. A stiffer material will have a larger value of Young’s modulus and will resist change in shape when stress is applied to it. Young’s modulus describes deformation along an axis.