Question

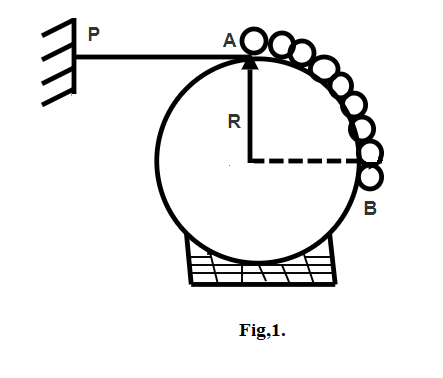
A uniform flexible chain of length $1.50cm$ rests on a fixed smooth sphere of radius $R=\dfrac{2}{\pi }m$ such that one end A Of chain is at top of the sphere while the other end B is hanging freely chain is held stationary by a horizontal thread PA as shown in figure 1. Calculate the acceleration of the chain when the thread is burnt.

Answer 1

Solution to this problem is obtained by newton’s laws of motion. The force which causes a change in velocity and change in velocity creates a force. Newton’s second law of motion to relate the motion of the object to the forces involved. Objects with constant masses are used in Newton’s second law.

Complete step-by-step solution:
Newton’s law of motion explains the relationship between motion of object and the force which is acting on the object. There are three newton’s laws of motion and that are newton’s first law, newton’s second law and newton’s third law.
Newton’s first law states that an object at rest continuous to be at rest and an object at motion continuous to be at motion until unless an external force acts on it and velocity of the object is constant when the net force on the body is zero. Newton’s first law is also called the principle of inertia.
Newton’s second law states that the rate of change of momentum of a body with respect to time is directly proportional to the applied force in the same direction as the applied force and inversely proportional to mass.
Force due to hanging ${{F}_{1}}=\dfrac{1}{2}mg$
Force supporting the motion is$=dmg\cos \theta$
Where $d=mdx$
$\theta =\dfrac{l}{r}dx$
$\begin{aligned} & {{F}_{2}}=rd\theta \times mg\cos \theta \\\ & {{F}_{2}}=rmg\int\limits_{0}^{\dfrac{\pi }{2}}{\cos \theta d\theta } \\\ & {{F}_{2}}=2g\dfrac{m}{\pi } \\\ \end{aligned}$
${{F}_{1}}=0.5mg$
So total force ${{F}_{1}}+{{F}_{2}}=mg(\dfrac{1}{2}+\dfrac{2}{\pi })$
Newton’s law of motion stated that acceleration of an object is directly proportional to net force and inversely proportional to mass
Acceleration=$\dfrac{netforce}{mass}$
$a=\dfrac{\sum{F}}{m}$
$a=\dfrac{4+\pi }{3\pi }.g$
$a=7.58m{{s}^{-2}}$
Acceleration of the chain when the thread is burnt is $7.58m{{s}^{-2}}$

Note: Students the acceleration of the chain is obtained by Newton's second law of motion. Acceleration depends on the mass and the force which acts on the body. The force velocity, acceleration and momentum have both magnitude and a direction. Heavier objects have less acceleration compared to lighter objects.