Solveeit Logo
Login

Question

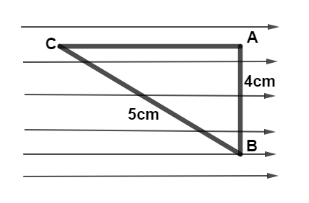
Question: A uniform electric field of \(800\,V{m^{ - 1}}\) is acting as shown. Given \(AB = 4cm\) \(BC = 5cm\)...

A uniform electric field of 800 Vm−1800\,V{m^{ - 1}} is acting as shown. Given AB=4cmAB = 4cm BC=5cmBC = 5cm. Find potential difference between points (i) AA and BB (ii) AA and CC (iii) BB and CC

Explanation

Solution

In electrostatics, electric field is the space around the charge where electric force can be experienced by another charges and potential difference between two points is the difference of electric potential between two points and these two quantities are related mathematically as dV=−dE⃗.dr⃗dV = - d\vec E.d\vec r where dE,drdE,dr are the electric field and position magnitudes and having dot product between these two vectors.

Complete step by step answer:
From the given figure, let’s find the length of AC by using Pythagoras theorem we have,
(BC)2=(AC)2+(AB)2{(BC)^2} = {(AC)^2} + {(AB)^2}
⇒25−16=(AC)2\Rightarrow 25 - 16 = {(AC)^2}
⇒AC=3cm\Rightarrow AC = 3cm

According to the question, the magnitude of the electric field is E=800 Vm−1E = 800\,V{m^{ - 1}}.
(i) Point A and B. Since point A and B lie in the same position in electric field direction hence net change in length dr=0dr = 0 so, the potential difference between point A and B is zero.

(ii) Point A and C. since, Point A and Point C are separated by a distance of dr=3cm=0.03mdr = 3cm = 0.03m in the direction of electric field hence, using
dV=−dE⃗.dr⃗dV = - d\vec E.d\vec r
⇒dV=−800×0.03\Rightarrow dV = - 800 \times 0.03
∴dV=−24V\therefore dV = - 24V

Hence, potential difference between point A and C is dV=−24VdV = - 24V.

(iii) Point B and C. since point B and C are separated by a distance of dr=5cm=0.05mdr = 5cm = 0.05m in the direction of electric field hence using,
dV=−dE⃗.dr⃗dV = - d\vec E.d\vec r
⇒dV=−800×0.05\Rightarrow dV = - 800 \times 0.05
∴dV=−40V\therefore dV = - 40V

Hence, potential difference between point B and C is dV=−40VdV = - 40V.

Note: It should be remembered that, negative sign of potential difference shows that it decreases with the increasing in electric field direction and basic unit of conversion are used as 1 cm=0.01 m1\,cm = 0.01\,m remember, always find the distance between two points in the direction of electric field in order to find the potential difference across them.