Question
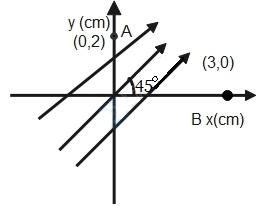
Question: A uniform electric field of 400 V/m is directed at 45∘ above the x-axis as shown in the figure. The ...
A uniform electric field of 400 V/m is directed at 45∘ above the x-axis as shown in the figure. The potential difference
VA−VB is given by:
Solution
The electric field is a unit vector. Firstly, the vector for the electric field is always expressed in terms of the vectors of sine and cosine angles. Then, the potential difference is expressed in terms of force and distance. By integrating the equations and substituting the limits, we will get the corresponding potential difference.
Complete answer:
Let E be the electric field
F be the force
F=400 V/m
The electric field vector makes an angle of x with the horizontal.
x=450
The horizontal component of force is
Fcosx
Similarly,
The vertical component of force is
Fsinx
In general,
The unit vector,
r^=cosxi^+sinxj^----(1)
Let this be equation (1)
Let the electric field vector be
E
The electric field vector is given as,
E=Fcosxi+Fsinxj ----(2)
Let this be equation (2)
Substitute the value of F and x in equation (2)
We get,
E=400cos45i+400sin45j---(3)
Let this be equation (3)
The value of
cos45=21----(4)
Let this be equation (4)
Similarly,
The value of
sin45=21 ---(5)
Let this be equation (5)
Substituting the equations (4) and (5) in equation (3)
We get,
E=400(21)i+400(21)j ---(6)
Let this be equation (6)
E=2002i+2002j---(7)
Let this be equation (7)
V=−∫F.dr---(8)
Let this be equation (8)
V=−∫2002(i+j)(dxi+dyj) ---(9)
Let this be equation (9)
V=−2002∫(dx+dy)---(10)
Let this be equation (10)
V=VB−VA ---(11)
Let this be equation (11)
Equating equations (10) and (11),
We get
VB−VA=−2002∫(dx+dy) ---(12)
Let this be equation (12)
VB−VA=−2002[∫dx+∫dy] ---(13)
Let this be equation (13)
Applying the limits at x and y,
We get,
VB−VA=−2002[∫03dx+∫20dy] ---(14)
Let this be equation (14)
VB−VA=−2002[(3−0)+(0−2)]
VB−VA=−2002(3−2)
VB−VA=−2002---(15)
Let this be equation (15)
Taking the negative on both the sides,
We get,
VA−VB=2002 ---(16)
Let this be equation (16)
Therefore,
VA−VB=2002mVcm---(17)
Let this be equation (17)
We know that
1m=100cm ---(18)
Let this be equation (18)
Substituting equation (18) in equation (17),we get,
VA−VB=2002100cmVcm
Cancelling cm, we get
VA−VB=2002100V
VA−VB=22V
VA−VB=2.8V
Therefore, the correct answer is D.2.8V
Note:
Electric field is always expressed as a vector quantity. If the angle of inclination of the force with the horizontal changes, the corresponding electric field vector also changes. It is also important to note that the conversion of values play a vital role in calculations. So, don’t forget to convert the ‘m’ to ‘cm’. Otherwise, the answer will be wrong.
