Question
Question: A uniform electric field of \[100V{{m}^{-1}}\] is directed at \({{30}^{\circ }}\) with the positive ...
A uniform electric field of 100Vm−1 is directed at 30∘ with the positive x - axis as shown in fig. Find the potential difference, VBA if OA=2m and OB=4m.
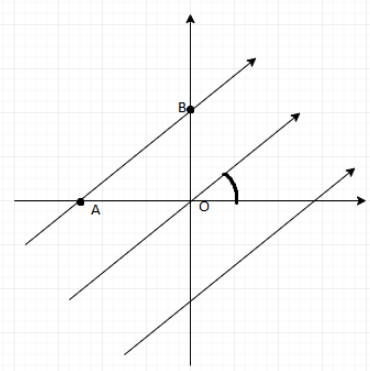
Explanation
Solution
We can find more information from the given figure by forming an equipotential surface that is perpendicular to the given electric field.
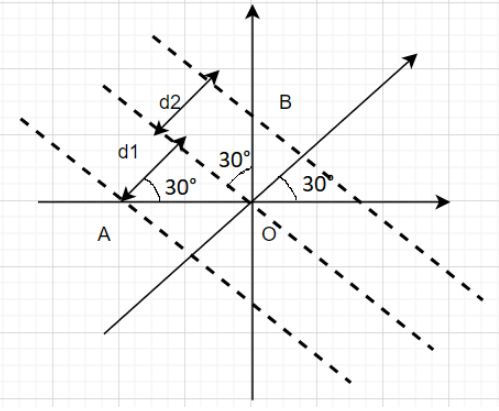
This forms two small right triangles within the figure. When we use its sides and angles, we can continue the calculation to find the potential difference.
Formulas used:
V=E×d
where V is the potential at a point, E is the electric field and d is the distance of separation.
Complete step by step answer:
From the modified figure,
VB−VA=100(3+2)V
