Question

A uniform electric field in the plane of the paper is shown in the figure. Here a, b, c, d are the points on the circle. ${{V}_{a}},{{V}_{b}},{{V}_{c}},{{V}_{d}}$ ​ are the potentials at those points respectively? Then :

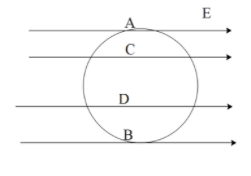
$\begin{aligned} & a){{V}_{a}}={{V}_{c}},{{V}_{b}}={{V}_{d}} \\\ & b){{V}_{a}}={{V}_{c}},{{V}_{b}}>{{V}_{d}} \\\ & c){{V}_{c}}>{{V}_{b}}={{V}_{a}}>{{V}_{d}} \\\ & d){{V}_{a}}={{V}_{b}},{{V}_{c}}={{V}_{d}} \\\ \end{aligned}$

Answer 1

The electric field is the electric force per unit charge. The direction of the field is taken to be the direction of force it is going to exert on a positive charge. The electric field will be outward from positive charge and inward to a negative charge same as magnetic lines of force. The electric field lines are directed from points at higher potential to points at lower potential.

Formula used:
$E=-\dfrac{dV}{dr}$

Complete step by step answer:
The electric field can be defined as the gradient of potential. That is, the electric field depends on potential in terms of the distance between the charge and the centre. The lines of electric fields are also directed from points at higher potential to points at lower potential. Clearly, we can observe from the diagram that,
The electric potential at c is for sure greater than the electric potential at d. As, the point d is lower than the point c.
Similarly, the electric field potential at a is greater than the electric field potential at d.
Therefore, the correct option is c which is,
${{V}_{c}}>{{V}_{b}}={{V}_{a}}>{{V}_{d}}$.

Additional Information:
As the test charge is moved along any axis through some distance, the rate of change in potential is the value of the electric field. An electric field exists only when there exists an electric potential difference. If the charge is uniform at all points, however high the potential is, there will not be any electric field. Thus, the relation between the electric field and electric potential can be generally expressed as- the electric field is the negative space derivative of the electric potential.

Note:
If there is uniform charge in a certain area, there will not be any electric field, however high the electric potential is. The electric field is positive if it is taken from lower potential to higher potential. The field direction is negative if the potential is taken from higher to lower potential.