Solveeit Logo
Login

Question

Question: A uniform electric field exists in xy plane. The potential of points A\[\left( {2,2} \right)\], B\[\...

A uniform electric field exists in xy plane. The potential of points A(2,2)\left( {2,2} \right), B(−2,2)\left( { - 2,2} \right) and C(2,4)\left( {2,4} \right) are 4V4{\rm{ V}}, 16V16{\rm{ V}}, 12V12{\rm{ V}} respectively. The electric field is
A. (4i^+5j^)V/Vmm\left( {4\hat i + 5\hat j} \right){\rm{ }}{{\rm{V}} {\left/ {\vphantom {{\rm{V}} {\rm{m}}}} \right. } {\rm{m}}}
B. (3i^+4j^)V/Vmm\left( {3\hat i + 4\hat j} \right){\rm{ }}{{\rm{V}} {\left/ {\vphantom {{\rm{V}} {\rm{m}}}} \right. } {\rm{m}}}
C. −(3i^+4j^)V/Vmm - \left( {3\hat i + 4\hat j} \right){\rm{ }}{{\rm{V}} {\left/ {\vphantom {{\rm{V}} {\rm{m}}}} \right. } {\rm{m}}}
D. (3i^−4j^)V/Vmm\left( {3\hat i - 4\hat j} \right){\rm{ }}{{\rm{V}} {\left/ {\vphantom {{\rm{V}} {\rm{m}}}} \right. } {\rm{m}}}

Explanation

Solution

Electric field in a direction is equal to the partial derivative of potential in that direction. The expression for the electric field of the given x-y plane is E→=Exi^+Eyj^\overrightarrow E = {E_x}\hat i + {E_y}\hat j. Here, Ex{E_x} and Ey{E_y} represent the electric field in x and y-direction, respectively.

Complete step by step answer:
Let us first show all the given points on the x-y plane. Here, the value of x and y is in meters.

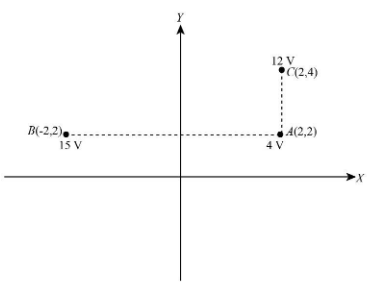
The electric field expression in the x-direction is equal to the negative value of the ratio of change of potential and change of length in the x-direction.
Ex=−ΔVxΔx{E_x} = - \dfrac{{\Delta {V_x}}}{{\Delta x}}……(1)
From the above graph, we can find:

Δx=2m−(−2m) ⇒Δx=4m\Delta x = 2{\rm{ m}} - \left( { - 2{\rm{ m}}} \right)\\\ \Rightarrow\Delta x = 4{\rm{ m}}

And,

ΔVx=4V−16V ⇒ΔVx=−12V\Delta {V_x} = 4{\rm{ V}} - 16{\rm{ V}}\\\ \Rightarrow\Delta {V_x} = - 12{\rm{ V}}

Substitute 4m4{\rm{ m}} for Δx\Delta x and −12V - 12{\rm{ V}} for ΔVx\Delta {V_x} in equation (1).

Ex=−(−12V)4m ⇒Ex=3V/Vmm{E_x} = - \dfrac{{\left( { - 12{\rm{ V}}} \right)}}{{4{\rm{ m}}}}\\\ \Rightarrow{E_x} = 3{\rm{ }}{{\rm{V}} {\left/ {\vphantom {{\rm{V}} {\rm{m}}}} \right. } {\rm{m}}}

The electric field expression in the y-direction is equal to the negative value of the ratio of change of potential and change of length in the y-direction.
Ey=−ΔVyΔy{E_y} = - \dfrac{{\Delta {V_y}}}{{\Delta y}}……(2)
Again, using the graph we can write:

Δy=4m−2m ⇒Δy=2m\Delta y = 4{\rm{ m}} - 2{\rm{ m}}\\\ \Rightarrow\Delta y = 2{\rm{ m}}

And,

ΔVy=12V−4V ⇒ΔVy=8V\Delta {V_y} = 12{\rm{ V}} - 4{\rm{ V}}\\\ \Rightarrow\Delta {V_y} = 8{\rm{ V}}

Substitute 2m2{\rm{ m}} for Δy\Delta y and 8V8{\rm{ V}} for ΔVy\Delta {V_y} in equation (2).

⇒Ey=−4V/Vmm\Rightarrow{E_y} = - 4{\rm{ }}{{\rm{V}} {\left/ {\vphantom {{\rm{V}} {\rm{m}}}} \right. } {\rm{m}}}

Let us now write the expression of the magnetic field in vector form.
E→=Exi^+Eyj^\overrightarrow E = {E_x}\hat i + {E_y}\hat j
Here i^\hat iand j^\hat j are unit vectors in x and y direction, respectively.
Substitute 3V/Vmm3{\rm{ }}{{\rm{V}} {\left/ {\vphantom {{\rm{V}} {\rm{m}}}} \right. } {\rm{m}}} for Ex{E_x} and −4V/Vmm - 4{\rm{ }}{{\rm{V}} {\left/ {\vphantom {{\rm{V}} {\rm{m}}}} \right. } {\rm{m}}} for Ey{E_y} in the above expression of the electric field.

E→=(3V/Vmm)i^+(−4V/Vmm)j^ ∴E→=(3i^−4j^)V/Vmm\overrightarrow E = \left( {3{\rm{ }}{{\rm{V}} {\left/ {\vphantom {{\rm{V}} {\rm{m}}}} \right. } {\rm{m}}}} \right)\hat i + \left( { - 4{\rm{ }}{{\rm{V}} {\left/ {\vphantom {{\rm{V}} {\rm{m}}}} \right. } {\rm{m}}}} \right)\hat j\\\ \therefore\overrightarrow E = \left( {3\hat i - 4\hat j} \right){\rm{ }}{{\rm{V}} {\left/ {\vphantom {{\rm{V}} {\rm{m}}}} \right. } {\rm{m}}}

Therefore, the expression for the electric field is (3i^−4j^)V/Vmm\left( {3\hat i - 4\hat j} \right){\rm{ }}{{\rm{V}} {\left/ {\vphantom {{\rm{V}} {\rm{m}}}} \right. } {\rm{m}}} , and option (D) is correct.

Note: Alternate method: We can assume the expression for the potential of any point (x, y). Substituting the individual values of x, y, and potential in that equation and solving them, we will get unknown quantities. On substituting the unknown quantities in the expression of potential, we can obtain the general expression of the potential and electric field.