Question
Question: A uniform electric field exists between two charged plates as shown in the figure. What should be th...
A uniform electric field exists between two charged plates as shown in the figure. What should be the work done in moving a charge q along the closed rectangular path ABCDA.
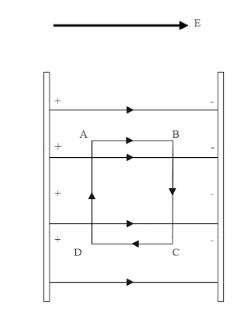
Solution
Work done is a property that depends on displacement of the object the force is subjected on. workdone=force×displacement . We need to find the displacement the charge travels through the loop ABCDA.
Formula Used: We will be using the notion that force is conservative and work done by an electric charge q in an uniform electric field E is given by w=Edcosθ where w is the work done by the charge, d is the displacement due to the force applied on the charge (which in this case is an electrostatic force), and θ is the angle between the two vectors.
Complete Step by Step solution
We know, in a uniform electric field the field lines are going to move from positively charged plate to the negatively charged one. Now suppose you are placing a charge in between the plates like shown in the figure below. Also consider an imaginary rectangular path ABCD with dimensions, AB=d1=CD and BC=d2=DA .
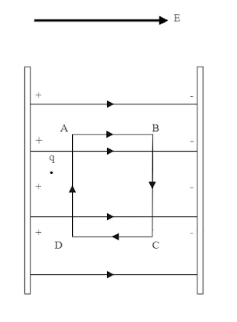
Now let us consider the work done to move the charge from point A to B between the plates.
w=Ed1cos0∘
Here θ=0∘ , because the work done on the point to move from A to B and the electric field lines are in the same direction.
We also know that, cos0∘=1 . So, w=Ed1(1)
w=Ed1
Similarly, along the path BC=d2 , the angle between the two vectors is, θ=90∘ . w=Ed2cos90∘
w=Ed2(0)
And thus, the work done to move charge on the path BC,
w=0J
Similarly for path CD we can see that the angle between the vectors θ is 180∘ . We know that cos180∘=−1 . Thus, making work done along the path CD, w=Ed1cos180∘ .
w=Ed1(−1)
w=−Ed1
Also, for the path DA, the angle θ is 270∘ . Thus, the work done can be given by w=Ed2cos270∘ . Now we can find the work done along the path DA as w=Ed2(0) . Since, cos270∘=0 .
w=0
Now that we have the work done to move the charge q along the closed path ABCDA. Let us calculate the total work done by adding the work done to move the charge along each side.
w=Ed1+0+(−Ed1)+0
w=0
Thus, the work done is zero. No actual work is done to move a charge around the closed path ABCDA as shown in the figure.
Note
Alternate solution-
Since we can see that the charge is supposed to travel along the path ABCDA. The particle starts from A and ends up back in A, thus making the displacement d=0 . Work is a quantity whose magnitude depends on the displacement, thus the work done is
w=Edcosθ
w=E(0)cosθ
Thus, making the work done zero. This simple logic can be used to solve the problem faster.
