Question

A uniform disc of radius R is put over another uniform disc of radius 2R of the same thickness and density. The peripheries of the two discs touch each other. The position of their centre of mass is

Answer 1

First of all draw the diagram according to question and then find the values of mass by using surface charge density for both spheres and then put the values in the required formula of centre of mass.

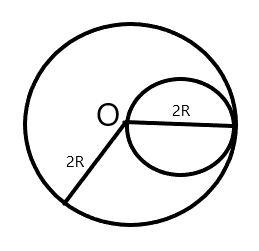
Complete step-by-step answer:
Here, in the question it is given that a uniform disc of radius R is put over another uniform disc of radius 2R as shown in the diagram as these two disc has same density.
So let σ be the surface charge density and it is defined as a mass per unit area.
Now let $M_1$ and $M_2$ are the masses of the spheres of radius R and 2R respectively. And as the area of disc is $A = \pi {R^2}$
Now, the surface charge density for disc of radius R is $\sigma = \dfrac{{{M_1}}}{{\pi {R^2}}}$
⇒ Mass of disc of radius R is ${M_1} = \sigma \times \pi {R^2}$
Similarly, the surface charge density for disc of radius 2R is $\sigma = \dfrac{{{M_2}}}{{\pi {{\left( {2R} \right)}^2}}}$
⇒ Mass of disc of radius 2R is ${M_2} = \sigma \times \pi {\left( {2R} \right)^2} = 4\pi {R^2}$
Now, centre of mass ${X_{cm}} = \dfrac{{{M_1}{X_1} + {M_2}{X_2}}}{{{M_1} + {M_2}}}$……………………….. (1)
Where, Xcm is the position of centre of mass
$X_1$ is the distance of disc of radius R from the origin O = R
$X_2$ is the distance of disc of radius 2R from origin O = 0
Put these values in the equation (1), we get
⇒ ${X_{cm}} = \dfrac{{\sigma \pi {R^2} \times R + 4\sigma \pi {R^2} \times 0}}{{4\sigma \pi {R^2} + \sigma \pi {R^2}}}$
⇒ ${X_{cm}} = \dfrac{R}{5}$
Hence, ${X_{cm}} = \dfrac{R}{5}$right to the corner of large disc

Note: It should be noted that in the question we have given the same charge density for two disc so σ should be the same for both disc. And the area of the disc is π$R^2$.