Question

A uniform disc of radius R and mass M is free to rotate about a fixed horizontal axis perpendicular to its plane and passing through its centre. A string wrapped over its rim and a block of mass m is attached to the free end of the string. The block is released from rest. If the string does not slip on the rim then find the acceleration of the block. Neglect the mass of the string.

Answer 1

Making free body diagrams of the body attached to the string and the uniform disc will help in solving the problem. We will use the formula of the angular acceleration ($\alpha$) given by: $\alpha =\dfrac{a}{R}$, where (a) will be the acceleration of the body of mass (m), since the string doesn’t slip. Equating the forces in the free body diagram will give: $mg-T=ma$ and finding the torque ($\tau$) of the disc will give: $\tau =I\alpha =TR$.

Step by step solution:
Let’s start by making a diagram as per the problem.

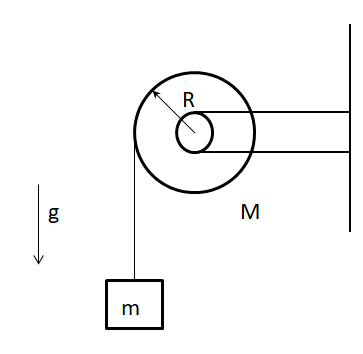
A massless string is attached to a body of mass (m), which is initially at rest. The string is passed over the ring of an uniform disc, having radius (R) and mass (M). The gravity (g) is acting downwards. As the body is released, it causes a tension (T) to form in the string as the body starts to fall downward with acceleration (a). Since, the string does not slip over the disc, it causes the disc to rotate.
Let’s make a free body diagram of the body of mass (m).

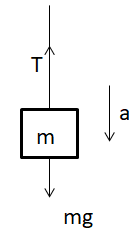
An upward tension acts on the string, attached to the body of mass (m). The weight of the body (mg) acts vertically downward. The overall acceleration of the body is downward, hence equating all the forces, we get: $mg-T=ma\Rightarrow T=mg-ma\to (1)$.
Let’s consider the free body diagram of the disc now.

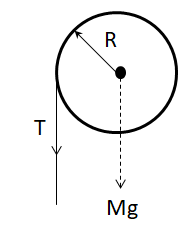
The tension on the string acts downwards, and the centre of the disc is the centre of mass of the body. The weight of the body (Mg) acts downwards from the centre of mass. Let the angular acceleration of the disc be ($\alpha$) given by: $\alpha =\dfrac{a}{R}$. The net torque acting on the body is given by: $\tau =I\alpha =T(\bot \text{ from C}\text{.M})+Mg(\bot \text{ from C}\text{.M})$, where $(\bot \text{ from C}\text{.M})$refers to the perpendicular distance from the centre of mass. Hence, the net torque acting on the disc becomes: $\tau =I\alpha =T(\bot \text{ from C}\text{.M})+Mg(\bot \text{ from C}\text{.M})\Rightarrow I\alpha =TR+Mg(0)\Rightarrow I\alpha =TR$.
Here, (I) is the moment of inertia of the disc, which is: $I=\dfrac{M{{R}^{2}}}{2}$.
Hence, the value becomes: $\left( \dfrac{M{{R}^{2}}}{2} \right)\alpha =TR\Rightarrow \left( \dfrac{M{{R}^{2}}}{2} \right)\dfrac{a}{R}=TR\Rightarrow T=\dfrac{Ma}{2}\to (2)$.
Solving the equations (1) and (2), we get: $\dfrac{Ma}{2}=mg-ma\Rightarrow Ma=2mg-2ma\Rightarrow a(M+2m)=2mg\Rightarrow a=\dfrac{2mg}{M+2m}$.
Therefore, the velocity with which the block will fall is: $a=\dfrac{2mg}{M+2m}$.

Note: We must remember that the acceleration of the body of mass (m) upon being released from rest is not g, but reduced value a, because the string isn’t slipping over the disc. Hence, there is a tension caused due to the rotational force of the disc, which reduces the acceleration of the body. Else, if the string was slipping over the disc, then there wouldn’t be any tension acting on the string.