Question
Question: A uniform disc of mass m, radius r and a point mass m are arranged as shown in the figure. The accel...
A uniform disc of mass m, radius r and a point mass m are arranged as shown in the figure. The acceleration of point mass is : (Assume there is no slipping between the pulley and thread and the disc can rotate smoothly about a fixed horizontal axis passing through its centre and perpendicular to its plane).
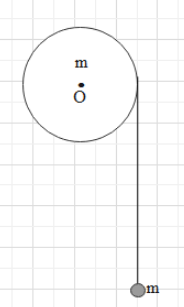
A. 2g
B. 3g
C. 32g
D. None of these
Solution
To solve the given question we must know about rotational mechanics. Calculate the torque and find the angular acceleration of the disc. With this find the tension in the rope and acceleration of the point mass.
Formula used:
τ=Fr⊥
τ=Iα
a=rα
Fg=mg
Fnet=ma
Complete step by step answer:
To the gravitational force acting on the point mass m in the downward direction, the point mass will accelerate downwards. Let its acceleration be a.Due to this, there will be a tension created in the thread. Let that tension be T.
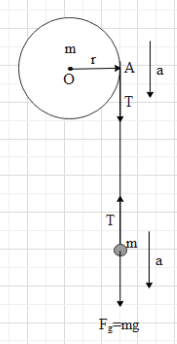
Then the tension in the rope will apply a torque on the disc. As a result, the disc will rotate about the fixed axis at the centre with some angular acceleration.
The magnitude of torque about an axis is given as τ=Fr⊥,
where F is the force acting on the disc,r⊥ is the perpendicular distance between the axis of rotation and the force.
In this case, F=T and r⊥=r.
⇒τ=Tr …. (i)
The torque is also given as τ=Iα ….. (ii),
where I is the moment of inertia of the body about the axis of rotation and α is the angular acceleration of the body.
The moment of inertia of a disc of mass m and radius r, about a fixed horizontal axis passing through its centre and perpendicular to its plane is equal to I=2mr2.
Substitute the value of I in (ii).
⇒τ=2mr2α …. (iii)
Now equate (i) and (iii).
⇒Tr=2mr2α
⇒α=mr2T …(iv)
The linear acceleration of the disc at point A will be a=rα
Substitute the value of α from (iv).
⇒a=r(mr2T)=m2T.
⇒T=2ma …. (v)
Since it is given that there is no slipping between the thread and the disc, the acceleration of the point mass will be a.
Now, let us find the net force on the point mass m.The gravitational force on the mass is Fg=mg, where g is acceleration due to gravity (as shown).
Therefore, the net force on the point mass is Fnet=Fg−T.
⇒Fnet=mg−T
And from Newton’s second law of motion Fnet=ma.
⇒ma=mg−T
Substitute the value of T from (v).
⇒ma=mg−2ma
⇒a+2a=g
∴a=32g
Therefore, the acceleration of the point mass is equal to 32g.
Hence, the correct option is C.
Note: A common mistake that can be done while solving the given question is that the students may assume that the tension in the string to be equal to the gravitational force acting on the point mass, i.e. T=mg. However, in that case the mass will be at rest, which is not possible.
