Question

A uniform disc of mass $m$ and radius $R$ is rotating with angular velocity $\omega$ on a smooth horizontal surface. Another identical disc is moving translationally with velocity$v$as shown. When they touch each other, they stick together. The angular velocity of the center of mass of the system contact will be:

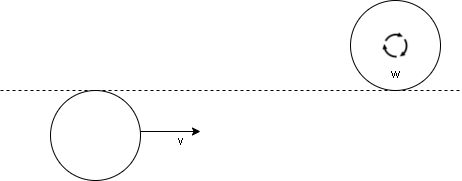
A) Zero
B) $\dfrac{{2v - R\omega }}{{6R}}$
C) $\dfrac{v}{R}$
D) $\dfrac{\omega }{{{R^2}}}$

Answer 1

Angular velocity is the velocity which relates how fast the position of an object changes with respect to time. It shows how fast an object moves relative to another point. It is given that another disc is moving translationally with respect to the first one. An object is said to be in translational motion if they are moving in the same line.

Complete step by step solution:
Step I:
If they are colliding with each other, then they should be following the law of conservation of energy. Since when two objects collide, their velocity can change and energy can be transformed from one form to another but can not be destroyed. Both the discs will have a moment of inertia before and after the collision.
Step II:
Let $I$ be the moment of inertia and $\omega$be the angular velocity before the collision.
Let ${I^{'}}$be the moment of inertia and ${\omega ^{'}}$ be the angular velocity when they stick together.
In translational motion, the kinetic energy of the discs is $\dfrac{1}{2}m{v^2}$.
Step III:
According to law of conservation of Energy,
Energy of discs before collision = Energy of discs after collision
$\dfrac{1}{2}{\omega^2} + \dfrac{1}{2}m{v^2} = \dfrac{1}{2}{I^{'}}{\omega ^{{{'}^2}}}$----(i)
Moment of Inertia is written as:
$\Rightarrow I = m{r^2}$and
Angular velocity is written as
$\Rightarrow \omega = \dfrac{v}{r}$
$\Rightarrow v = \omega r$
Step IV:
Substituting value of $I$and$v$in equation (i),
$\Rightarrow \dfrac{1}{2}m{r^2}{\omega ^2} + m{r^2}{\omega ^2} = \dfrac{3}{2}m{r^2} \times 2\omega {'^2}$
$\Rightarrow \dfrac{{{\omega ^2}}}{2} + {\omega ^2} = 3\omega {'^2}$
$\Rightarrow \omega {'^2} = \dfrac{1}{2}{\omega ^2}$
$\Rightarrow \omega {'} = \dfrac{\omega }{{\sqrt 2 }}$
$\Rightarrow \omega ' = \dfrac{\omega }{{{2^2}}}$

$\therefore$The angular velocity of the center of mass will be $\dfrac{\omega }{{{2^2}}}$. Hence, option D is the correct answer.

Note:
It is to be noticed that translational motion is not similar to linear motion. They both are different and are not to be mixed. Linear motion is a type of translational motion because in this motion the object moves in a straight line only. But in translational motion, the object can move in two or three dimensions also.