Question
Question: A uniform disc of mass M= 1 kg, radius R= 1m is moving towards right on smooth horizontal surface wi...
A uniform disc of mass M= 1 kg, radius R= 1m is moving towards right on smooth horizontal surface with velocity vs=20m/s and having velocity ω0=4rad/s about the perpendicular axis outward the plane of disc passing through the center of disc. Suddenly the top point of the disc gets hinged about a fixed smooth axis. The angular velocity (in rad/s) of disc about new rotation axis is:
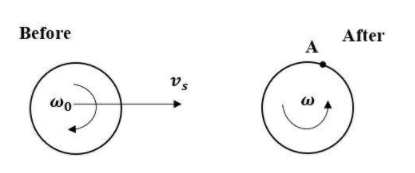
Solution
To solve this problem, first find the moment of inertia of disc. Then, using the relation between angular momentum, moment of inertia and angular velocity, find the value of angular momentum. Use the relation between torque and angular acceleration to find angular acceleration. Then, use the angular kinematic equation and substitute the values. This will give the angular velocity of the disc about the new rotation axis.
Complete answer:
Given: M= 1 kg
R= 1 m
vs=20m/s
ω0=4rad/s
Moment of Inertia is given by,
I=21MR2
Substituting the values in above equation we get,
I=21×1×12
∴I=21
Thus, the moment of inertia of the disc is 21kg/m2.
We know, angular momentum is given by,
L=Iω
Substituting values in above equation we get,
L=21×4
∴L=2kg/m2/s.
But, we know, torque is equal to the change in angular momentum.
∴τ=2Nm
But, we also know, τ=Iα
∴2=21α
∴α=4rad/s2
From angular kinematics we know,
ω2=ω1+αt
But, v=tr
∴ω2=ω1+αvr
Now, substituting the values in above equation we get,
ω2=0.2rad/s
Hence, the angular velocity of the disc about the new rotation axis is 0.2 rad/s.
Note:
Students should know all the angular or rotational kinematic equations. They should also know the proper application of those equations. To choose the rotational kinematic equation, figure out which variables are given in the question and which are asked.
Example: ω=ω0+αt
If any three variables of these are given, then you can use this relation to find the fourth variable.
