Question

A uniform disc is acted upon by two equal forces of magnitude F. One of them acts tangentially on the disc while the other is acting at the central point of the disc. The friction between the disc surface and ground surface is nF. If r is the radius of the disc the value of n would be? (in N)
a)0
b)1.2
c)2.0
d)3.2

Answer 1

In the above question it is given to us that the disc is acted by two different forces one at the center and the other tangential force. First we will obtain the equation of motion of the above disc. Further we will consider the case of pure rolling of the disc and accordingly determine the value of n.

Formula used:
$I=\dfrac{M{{R}^{2}}}{2}$
$\tau =I\alpha$
${{F}_{NET}}=ma$
$a=\alpha R$

Complete step by step answer:

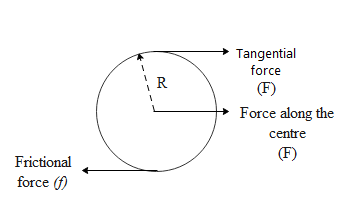
In the above diagram we can see the action of different forces on the disc of radius ‘R’. If the net force on the above disc is ${{F}_{NET}}=ma$ where a is the linear acceleration of the disc and m is the mass of the disc we can write,
$\begin{aligned} & {{F}_{NET}}=2F-f \\\ & ma=2F-f...(1) \\\ \end{aligned}$
In the above figure if we observe the disc will rotate about its center due to the action of torque due to the tangential force and that of the frictional force. If the moment of inertia of the disc is I and the angular acceleration is $\alpha$, than the torque $\tau$ is given by,
$\tau =I\alpha$
By definition of torque it is defined as the tangential force times the perpendicular distance from the center. Hence from this we can write net torque on the disc as,
$\begin{aligned} & \tau =(F+f)R \\\ & \Rightarrow \dfrac{I\alpha }{R}=(F+f) \\\ & \Rightarrow F=\dfrac{I\alpha }{R}-f...(2) \\\ \end{aligned}$
For a circular disc of uniform mass m, the moment of inertia about the centre of the disc is given by,
$I=\dfrac{M{{R}^{2}}}{2}$. Let us say we consider the case of pure rolling. Then the relation between angular acceleration and linear acceleration is equal to $a=\alpha R$. Substituting this obtained results in equation 2 we get,
$\begin{aligned} & F=\dfrac{I\alpha }{R}-f \\\ & F=\dfrac{(m{{R}^{2}}/2)(a/R)}{R}-f \\\ & \Rightarrow F=\dfrac{m{{R}^{2}}a}{2{{R}^{2}}}-f=\dfrac{ma}{2}-f \\\ & \Rightarrow F+f=\dfrac{ma}{2}...(3) \\\ \end{aligned}$
Solving equation 1 and 3 we get value of F as $\dfrac{ma}{2}$
If we plug this value back in equation 3 we get,
$\begin{aligned} & F+f=\dfrac{ma}{2} \\\ & \Rightarrow \dfrac{ma}{2}+f=\dfrac{ma}{2} \\\ & \therefore f=0 \\\ \end{aligned}$
And since f=nF we can say that the value of n is also zero.

So, the correct answer is “Option A”.

Note:
It is to be noted that the value of F is non zero. Therefore we could say that the value of n is zero. In the above solution we have considered the disc to be in pure rolling condition. Hence the above conditions hold valid only in case of pure rolling.