Question
Question: A uniform cylinder of radius rolls over a horizontal plane passing into an inclined plane forming an...
A uniform cylinder of radius rolls over a horizontal plane passing into an inclined plane forming an angle α=30∘ with the horizontal. Find the maximum value of the velocity v0 which still permits the cylinder to roll onto the inclined plane section without a jump. The sliding is assumed to be absent.
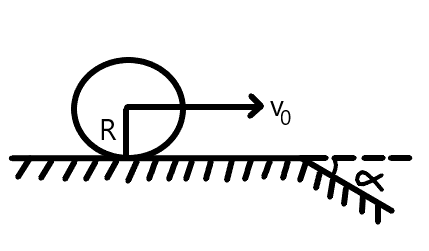
Solution
Hint : here, we will use the center of mass of the cylinder because it is moving on the plane without sliding. Also, we will use the law of conservation of energy and parallel axis theorem to find the value of the velocity. Here, {v_0} will be the maximum velocity that will permit the cylinder to roll onto the cylinder.
Complete Step By Step Answer:
Now, as we know that the cylinder will move without sliding, the center of the cylinder will rotate through the point O, while passing through the common edge of the planes. In other words, the point O will become the foot of the instantaneous axis of rotation of the cylinder.
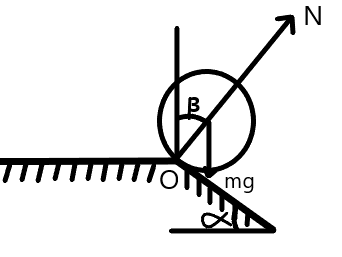
At any instant, let v1 be the velocity of the center of mass of the ring during the sliding of the ring when the angle will be β . Therefore, we have
Rmv12=mgcosβ−N
Here, let N be the normal reaction of the edge.
⇒v12=gRcosθ−mNR
Now, from the conservation law of energy, we get
21I0R2v12−21I0R2v02=mgR(1−cosβ)
But from the parallel axis theorem, we got the value of I0 which is given below
I0=2mR2+mR2=23mR2
Now, putting this value of I0 in the above equation, we get
21(23mR2)R2v12−21(23mR2)R2v02=mgR(1−cosβ)
⇒43mv12−43mv02=mgR(1−cosβ)
⇒43v12−43v02=gR(1−cosβ)
⇒43(v12−v02)=gR(1−cosβ)
⇒v12−v02=34[gR(1−cosβ)]
⇒v12=v02+34[gR(1−cosβ)]
Now, equating both the equations of v12 , we get
v02=3gR(7cosβ−4)−mNR
Here, N0 is the corresponding reaction of the edge.
vmax=3gR(7cosβ−4)−mNR
Here, the angle β will be smaller than or equal to α , therefore, we will replace β by α . Therefore, the above equation will become
vmax=3gR(7cosα−4)−mNR
Therefore, the maximum value of the velocity v0 which still permits the cylinder to roll onto the inclined plane section without a jump is 3gR(7cosα−4)−mNR .
Note :
Here, remember that N will be greater than N0 . Now, if N0 will be greater than zero than the cylinder will not jump while moving downwards. Thus, we can also say that the value of v0 will be less than vmax .
