Question
Question: A uniform cylinder of radius \(R\) is spinned about its axis to the angular velocity \({\omega _ \ci...
A uniform cylinder of radius R is spinned about its axis to the angular velocity ω∘ and then placed into a corner (figure shown). The coefficient of friction between the corner walls and the cylinder is equal to k. The number of turns the cylinder accomplish before it stops is given by η=xπk(1+k)gω∘2(1+k2)R. Find the value of x.
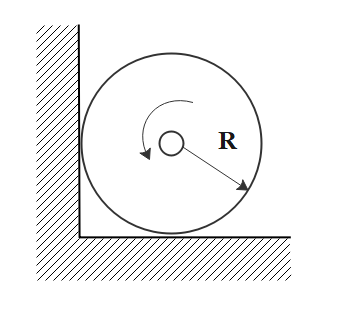
Solution
Angular velocity of an object is defined as the rate of velocity at which an object or a particle is rotating around a center or a specific point in a given time period. We need to apply the concept of angular velocity and translational equilibrium in order to obtain the required answer.
Complete step by step solution:
An object is said to be in a translational equilibrium if the velocity of its translational motion is constant. An object which is not moving, or which is moving in a straight line with a constant velocity is considered in translational equilibrium. In the problem, the rigid body is in translational equilibrium but there is an angular retardation. We will first sketch the free body diagram of the cylinder. We know that the frictional forces acting on the cylinder are kinetic. From the condition of the translational equilibrium for the cylinder,
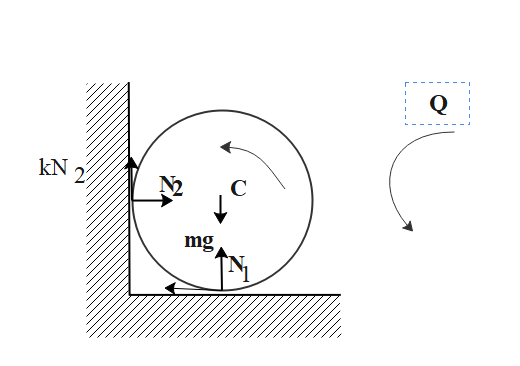
mg=N1=kN2 ; N2=kN1
Thus, N1=1+k2mg ; N2=k1+k2mg
For pure rotation of the cylinder about its rotational axis, Nz=Iβz
⇒−kN1R−kN2R=2mR2βz
⇒1+k2−kmgR(1+k)=2mR2βz
⇒βz=(1+k2)R2k(1+k)g
Now, from kinematical equation,
ω2=ω2∘+2βzΔφ
We have, Δφ=4k(1+k)gω∘2(1+k2)R , because ω=0
Therefore, the number of turns,
η=2πΔφ=8πk(1+k)gω∘2(1+k2)R
The number of turns the cylinder accomplish before it stops is given by η=xπk(1+k)gω∘2(1+k2)R
So, from comparing the given two quantities we get the value of x=8.
Hence, the value of x is 8.
Note: Similarly, like translational equilibrium, the rotational equilibrium is defined as the body in which the net torque acting on it will be equal to zero. In rotational motion the concept remains the same as in the translational motion. For conversion of a translational equation into rotational just convert the variables of translational motion into their respective rotational equivalent.
