Question
Question: A uniform cylinder of radius r and mass m can rotate freely about a fixed horizontal axis. A thin co...
A uniform cylinder of radius r and mass m can rotate freely about a fixed horizontal axis. A thin cord of length l and mass m0is wound on the cylinder in the single layer. Find the angular acceleration of the cylinder as a function of the length of x of the hanging part of the cord. The wound part of the cord is supposed to have a center of gravity on the cylinder axis as shown in figure
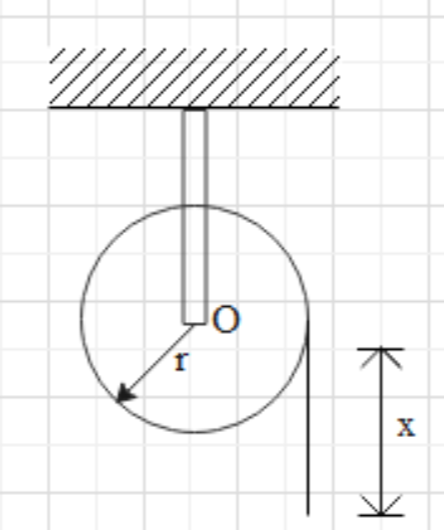
Solution
We have to find the acceleration of the cylinder in terms of the length of the cord which is unwounded by the cylinder and hanging from it. Now the cylinder can rotate so it can have torque. The torque can be given as the rate of change of angular momentum. By using the formula of torque we can find the relation between the length of the hanging part of the cord and the angular acceleration.
Formula used:
