Question

A uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density $\sigma$ at equilibrium position. The extension ${x_0}$ of the spring when it is in equilibrium, is
${\text{A}}{\text{. }}\dfrac{{Mg}}{k}\left( {1 - \dfrac{{LA\sigma }}{M}} \right) \\\ {\text{B}}{\text{. }}\dfrac{{Mg}}{k}\left( {1 - \dfrac{{LA\sigma }}{{2M}}} \right) \\\ {\text{C}}{\text{. }}\dfrac{{Mg}}{k}\left( {1 + \dfrac{{LA\sigma }}{M}} \right) \\\ {\text{D}}{\text{. }}\dfrac{{Mg}}{k} \\\$

Answer 1

First, we should draw a free body diagram for the cylinder to see the directions of the forces acting on the cylinder and get an equation of motion for the cylinder. By solving the obtained equation for the extension in the spring, we can get the required answer.
Formula used:
The buoyant force on a cylinder of surface area A and length L submerged fully in a liquid of density $\rho$ is given as
${F_B} = \sigma LAg$

Complete answer:
We are given a uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density $\sigma$ at equilibrium position.
Following is the free body diagram for the cylinder which shows the forces acting on the cylinder after it is half-submerged in the given liquid.

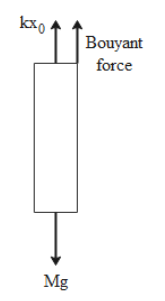
The mass of the cylinder is M so the force due to weight of the cylinder is Mg acting in downward direction. It is suspended by a spring whose spring constant is k. After half-submerging the cylinder in the liquid of density $\rho$, an upward buoyant force acts on the cylinder and the spring has an extension of ${x_0}$.
Now we can write the following equation based on the directions of the forces.
$k{x_0} + {F_B} = Mg$
Here ${F_B}$ is the buoyant force which is given as
${F_B} = \sigma \times \dfrac{L}{2} \times Ag$
Using this expression in the equation of motion, we get
$k{x_0} + \sigma \times \dfrac{L}{2} \times Ag = Mg$
Now solving for ${x_0}$, we get
${x_0} = \dfrac{1}{k}\left( {Mg - \dfrac{{\sigma LAg}}{2}} \right) \\\ {x_0} = \dfrac{{Mg}}{k}\left( {1 - \dfrac{{\sigma LAg}}{{2Mg}}} \right) \\\ {x_0} = \dfrac{{Mg}}{k}\left( {1 - \dfrac{{\sigma LA}}{{2M}}} \right) \\\$

This is the required answer. Hence, the correct answer is option B.

Note:
We have used $\dfrac{L}{2}$ in the expression for the buoyant force because only half of the length of the cylinder is submerged in the liquid. The buoyant force depends only on that part of the cylinder which is submerged in the liquid.